この記事では書籍「世界一美しい錯視アート」に掲載されている「太陽」という作品をProcessingを使って再現してみます。
太陽
今回作成した錯視アート「太陽」です。ただ、今回は書籍の「太陽」とはちょっと(だいぶ?)違っています。たぶん、パラメータを調整すれば、もっと近づけることができると思うのですが、試行錯誤中です。

書籍では「太陽がギラギラ拡大して見える。」と解説されています。確かに、そのように見えます。
描き方のポイント
とげとげの部分は凧型の図形を重ねて作る
この作品「太陽」ですが、一見すると非常に複雑な図形に見えますが、実は結構単純な構造をしています。つまり、下図のように各太陽のとげとげの部分は凧型の図形を重ねて作ったものになります。(なお、書籍の「太陽」に近づけていくためにはこの凧型の形をもう少し調整する必要があるでしょう。)
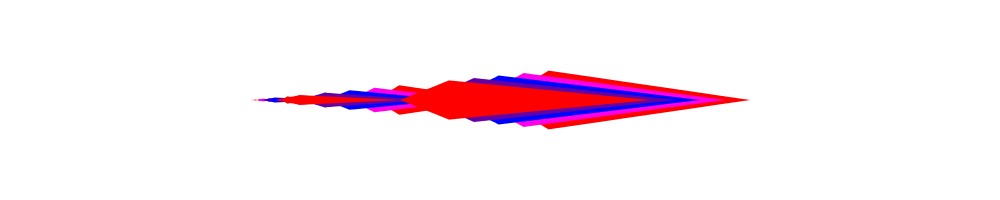
このとげ部分を円形に並べていくことで太陽の原型を作ることができます。
太陽の重なりはちょっと複雑
個々の太陽はその中心に青色または緑色で塗りつぶされた円を描くことで完成します。後は太陽を並べるだけです。中心の円の色に注目すると、どうもV字型に交互に並べられていると推測できました。ただ、書籍の「太陽」をよくよく見てみると、太陽同士の重なりはちょっと複雑で、重ね方の法則を見出そうとしましたが、できませんでした。
そこで今回は、太陽の重なりの順番に、太陽の位置とその中心にある円の色を配列に格納して使うことにしました。
プログラムコード
今回作成した錯視アート「太陽」のプログラムコードを載せておきます。
void setup() {
size(1000, 750);
background(255,255,255);
float line_len = width/2.0/4.0; // 太陽の図形の大きさ(中心からの最大距離)
float segment_len_initial = line_len / 2.0; // 凧型図形と次に小さい凧型図形の距離の初期値
float ratio = 1.0 - segment_len_initial / line_len; // 縮小比率
color col_b = color(0, 0, 255); // 太陽の図形の中心位置にある円の色(青色)
color col_g = color(0, 255, 0); // 太陽の図形の中心位置にある円の色(緑色)
// 太陽の図形の位置に関する配列
float[] pos_x = {width/8.0, 2.0*width/8.0, 4.0*width/8.0, 7.0*width/8.0, 2.0*width/8.0, 3.0*width/8.0, 4.0*width/8.0, 5.0*width/8.0, 1.0*width/8.0, 3.0*width/8.0, 5.0*width/8.0, 6.0*width/8.0, 6.0*width/8.0, 7.0*width/8.0, 1.0*width/8.0, 3.0*width/8.0, 5.0*width/8.0};
float[] pos_y = {width/8.0, 4.0*width/8.0, 4.0*width/8.0, 5.0*width/8.0, 2.0*width/8.0, 1.0*width/8.0, 2.0*width/8.0, 1.0*width/8.0, 3.0*width/8.0, 3.0*width/8.0, 3.0*width/8.0, 2.0*width/8.0, 4.0*width/8.0, 3.0*width/8.0, 5.0*width/8.0, 5.0*width/8.0, 5.0*width/8.0};
// 太陽の図形の中心位置にある円の色に関する配列
color[] pos_col = {col_g, col_g, col_b, col_b, col_g, col_b, col_b, col_g, col_b, col_g, col_b, col_g, col_g, col_g, col_g, col_b, col_g};
// 太陽の図形を配列の順番で描いていく
noStroke();
for(int i=0; i<pos_x.length; i++){
resetMatrix();
translate(pos_x[i], pos_y[i]);
drawSun(line_len, segment_len_initial, ratio, pos_col[i]);
}
save("suns.jpg");
}
// 太陽の図形を描く関数
void drawSun(
float line_len, // 線全体の長さ(中心からの長さの初期値)
float segment_len_initial, // 凧型図形と次に小さい凧型図形の距離の初期値
float ratio, // 縮小比率
color col // 中心の円の色
){
int line_num = 32; // 放射線状に拡がる図形の数
rotate(radians(360.0/line_num/2.0)); // 放射線状の拡がり角度の半分だけ回転させる
for(int i=0; i<line_num; i++){
rotate(radians(360.0/line_num));
drawLights(line_len, segment_len_initial, ratio, radians(360.0/line_num/2.0)); // 放射線状に拡がる図形を描く
}
// 中心に円を描く
fill(col);
circle(0.0, 0.0, 2.0*line_len/10.0);
}
// 放射線状に拡がる図形を描く関数
void drawLights(
float line_len, // 線全体の長さ(中心からの長さの初期値)
float segment_len_initial, // 凧型図形と次に小さい凧型図形の距離の初期値
float ratio, // 線分の縮小比率
float theta // 収束点での角度
){
float[] r = new float[10]; // 図形の中心と凧型図形の一番離れた点の距離に関する配列
float segment_len; // 凧型図形と次に小さい凧型図形の距離
r[0] = line_len; // 中心からの距離
segment_len = segment_len_initial; // 凧型図形と次に小さい凧型図形の距離
// 図形の中心と凧型図形の一番離れた点の距離に関する配列
int i = 0;
while(i<10-1){
i++;
r[i] = r[i-1] - segment_len;
segment_len = segment_len * ratio;
}
float gap = line_len / 20.0; // 凧型図形のずらし幅
float px, py;
float r1, r2;
noStroke();
for(int j=0; j<5; j++){
if( j == 1 ){
fill(#FF00E6); // ピンク色
} else if( j == 2 ){
fill(0,0,255); // 青色
} else if( j == 3 ){
fill(#6500A5); // 紫色
} else {
fill(255,0,0); // 赤色
}
i=0;
// 凧型図形を小さい方から順番に作っていく
while(i<10-1){
r1 = r[9-i]-gap*j;
if( r1 > 0.0 ){
r2 = r[9-i-1]-gap*j;
px = (r1+(r2-r1)/5.0) * cos(theta);
py = (r1+(r2-r1)/5.0) * sin(theta);
pushMatrix();
beginShape();
vertex(r1, 0.0);
vertex(px, -py);
vertex(r2, 0.0);
vertex(px, py);
endShape(CLOSE);
popMatrix();
}
i++;
}
}
}