薔薇攻撃

  1. ホーム
  2. 錯視アート
  3. 薔薇攻撃

この記事では書籍「世界一美しい錯視アート」に掲載されている「薔薇攻撃」という作品をProcessingを使って再現してみます。

薔薇攻撃

今回作成した錯視アート「薔薇攻撃」です。

薔薇攻撃

この作品を最初に見たとき、衝撃を受けました。最初螺旋を描いているのかと思いましたが、よくよく見てみると、三角形や長方形で作られた図形がくっついている同心円が並んでいるだけでした。何度見ても不思議に思います。

書籍では「同心円がゆがんでギラギラして見える。」と解説されています。

描き方のポイント

円上の三角形をどのように配置していくか

この作品「薔薇攻撃」では、円上に三角形をどのように並べていくかがポイントとなってきます。最初は各円上に三角形を並べたものを回転、縮小していって同心円を並べることを考えましたが、よく見ると三角形の配置は円上ではなく、放射線状にパターンがあることがわかりました。実際、放射線方向への三角形の並び方は4パターンあり、これらのパターンが順に繰り返されていることがわかりました。以下の図（左）にその4パターンを描いています。

三角形の並びは4パターン（左）、各図形の大きさの比率（右）

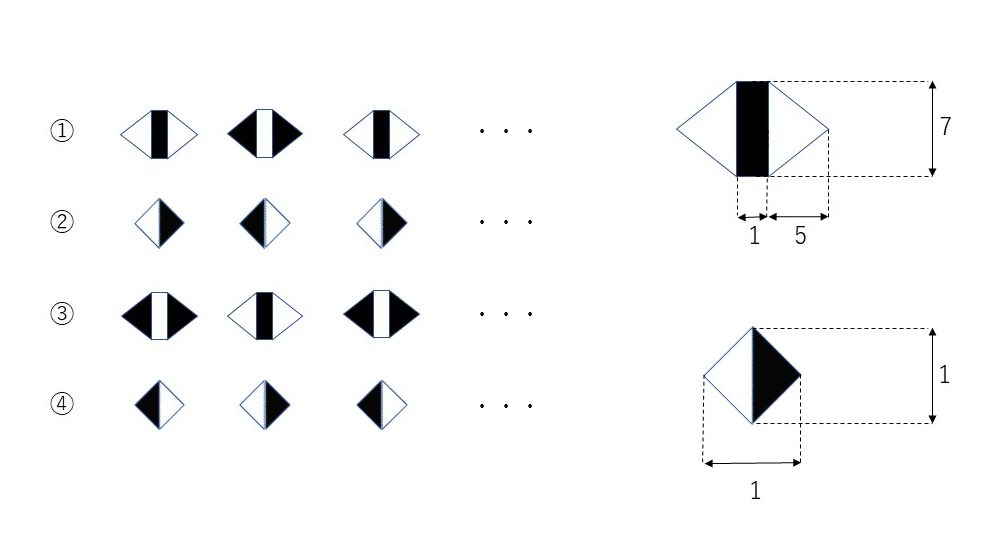
なお、今回描いた図形では、三角形の大きさの比率について図（右）のようにとりました。

プログラムコード

今回作成した錯視アート「薔薇攻撃」のプログラムコードを載せておきます。

void setup() {
  size(1000, 1000);

  noStroke();
  translate(width/2, height/2);
  
  background(#EA0231); // 背景色は赤色

  float radius_out = width/2.0 - width/30.0; // 一番外側の円の半径（収束点からの長さの初期値）
  float segment_len_initial = width/10; // 一番外側の円と2番目の外側の円の半径の差
  float ratio = 1.0 - segment_len_initial / radius_out; // 長径の縮小比率
  
  int triangles_num = 120; // 円周に並ぶ三角形の数
  float th1 = radians(360.0/triangles_num/2.0); // 三角形の底辺の長さを決めるための角度
  for(int i=0; i<triangles_num; i++){
    drawTriangles(radius_out, segment_len_initial, ratio, th1, i%4); // 放射線状に三角形を並べる
    rotate(radians(360.0/triangles_num));
  }
 
  save("roseattack.jpg");
}

// 放射線状に三角形を並べていく関数
void drawTriangles(
  float radius_out, // 一番外側の円の半径（収束点からの長さの初期値）
  float segment_len_initial, // 一番外側の円と2番目の外側の円の半径の差
  float ratio, // 線分の縮小比率
  float theta, // 収束点での角度
  int number // 三角形を並べる順番を調整する変数
//float xs, float as, int num){
){
  float x; // 円の半径
  float segment_len; // 隣り合う内側の円との半径の差

  x = radius_out;
  segment_len = segment_len_initial;

  float y1;
  int i = 0;  
  while(i<100){
    noStroke();
    y1 = x * sin(theta); // 三角形の底辺（の半分）の長さ
    if (number == 0){
      if( i%2 == 0 ){
        fill(255,255,255);
      } else {
        fill(0,0,0);
      }
      triangle(x+y1/7.0, y1, x+y1/7.0, -y1, x+y1*11.0/7.0, 0.0);
      triangle(x-y1/7.0, y1, x-y1/7.0, -y1, x-y1*11.0/7.0, 0.0);
      if( i%2 == 0 ){
        fill(0,0,0);
      } else {
        fill(255,255,255);
      }
      rectMode(CENTER);
      rect(x, 0.0, y1*2.0/7.0, y1*2.0);
    } else if ( number == 1 ) {
      fill(255,255,255);
      triangle(x, y1, x, -y1, x+y1, 0.0);
      fill(0,0,0);
      triangle(x, y1, x, -y1, x-y1, 0.0);      
    } else if ( number == 2 ) {
      if( i%2 == 0 ){
        fill(0,0,0);
      } else {
        fill(255,255,255);
      }
      triangle(x+y1/7.0, y1, x+y1/7.0, -y1, x+y1*11.0/7.0, 0.0);
      triangle(x-y1/7.0, y1, x-y1/7.0, -y1, x-y1*11.0/7.0, 0.0);
      if( i%2 == 0 ){
        fill(255,255,255);
      } else {
        fill(0,0,0);
      }
      rectMode(CENTER);
      rect(x, 0.0, y1*2.0/7.0, y1*2.0);
    } else {
      fill(0,0,0);
      triangle(x, y1, x, -y1, x+y1, 0.0);
      fill(255,255,255);
      triangle(x, y1, x, -y1, x-y1, 0.0);
    }

    x = x - segment_len; // 円の半径を更新
    segment_len = segment_len * ratio; // 隣り合う内側の円との半径の差を更新
    i++;
  }
}

コメントを残す