ここでは、P3M1のパターンで渦巻き図形による壁紙アートを作成しています。結果は以下のようになりました。

この壁紙アートにおける基本図形とタイルは以下のようなものです。タイルは基本図形を順に120°回転させたものを3つ組み合わせて作成しています。
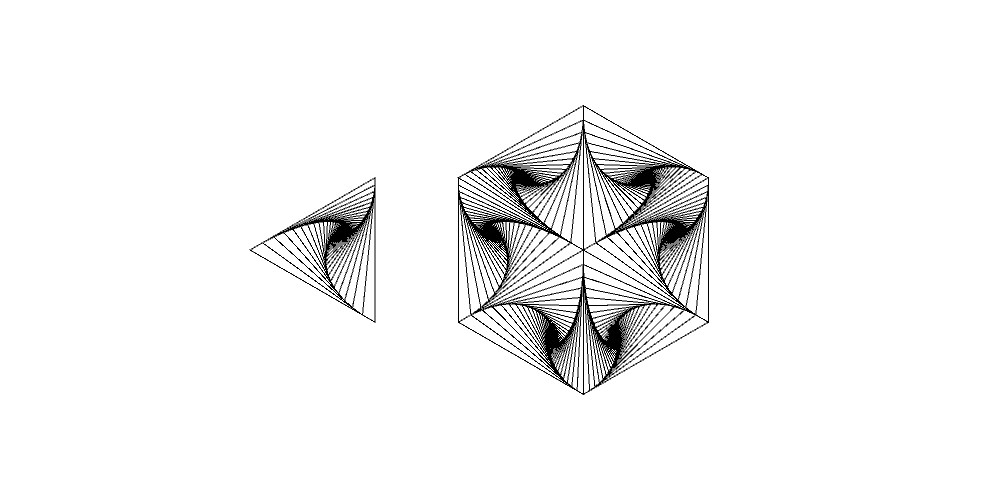
以下、この図形を描画するためのプログラムソースコードを載せておきます(Processingで動きます)。
PVector[][] lattice; // 格子点ベクトル
PShape tile; // タイル
PVector[] base = new PVector[2]; // 格子を張るベクトル
int col_num = 4; // 描画するタイルの列の数
float scalar; // タイルの辺の長さ
void setup(){
size(1000,1000);
scalar = width * 1.0 / col_num; // 描画ウィンドウと列の数からタイルの大きさを決定
makeTriangleVector(); // 三角格子を張るベクトルの生成
makeLattice(); // 格子点ベクトルを生成
makeTileP3M1(); // タイルを生成
drawTiling(); // タイリングを描画
save("P3M1_spiral.jpg");
}
// 三角格子を張るベクトルを生成する関数
void makeTriangleVector(){
base[0] = PVector.fromAngle(0.0);
base[1] = PVector.fromAngle(PI / 3);
}
// 三角格子を生成する関数
void makeLattice(){
int row_num = ceil(col_num / base[1].x); // 行の数
lattice = new PVector[col_num + 3][row_num + 1];
for (int i = 0; i < col_num + 3; i++){
for (int j = 0; j < row_num + 1; j++){
PVector v = PVector.mult(base[0], i * scalar);
v.add(PVector.mult(base[1], j * scalar));
lattice[i][j] = new PVector(v.x % ((col_num+3)*scalar) - 2 * scalar, v.y); // x軸方向にscalarの2倍だけ左にシフト
}
}
}
// 再帰的な正三角形を生成する関数(基本図形)
PShape makeRecurTriangle(){
float gap = 0.1; // 再帰的な正三角形を作るパラメータ
PVector[] v = new PVector[3]; // 正三角形の頂点
v[2] = new PVector(0,0);
for (int i=0; i<2; i++){
v[i] = PVector.fromAngle(i * PI / 3 - PI / 6);
v[i].mult(scalar / sqrt(3));
}
PShape tri = createShape();
tri.beginShape(TRIANGLES); // 3点ずつの頂点から三角形を作る
while( v[0].dist(v[1]) > 1){
for (int i=0; i<3; i++){
tri.vertex(v[i].x, v[i].y);
}
v = getVector(v, gap); // gapの分だけずらした正三角形の頂点を取得
}
tri.endShape();
return tri;
}
PVector[] getVector(PVector[] v, float gap){
PVector[] nextVec = new PVector[3];
for (int i=0; i<3; i++){
PVector dir = PVector.sub(v[(i+1)%3], v[i]);
if(i == 0){
dir.mult(gap/2.0); // 図形の形状を少しずつ変形していく
} else {
dir.mult(gap);
}
nextVec[i] = PVector.add(v[i], dir);
}
return nextVec;
}
// タイルを生成する関数
void makeTileP3M1(){
tile = createShape(GROUP); // PShapeのグループを作る
for (int i=0; i<2; i++){
for (int j=0; j<3; j++){
PShape tri = makeRecurTriangle(); // 再帰的な正三角形の生成
tri.rotate(2 * PI * j / 3); // 120度回転
tri.scale(pow(-1, i), 1); // y軸を中心に鏡映
tile.addChild(tri); // グループに追加
}
}
}
// 格子形状に合わせたタイリングを描画する関数
void drawTiling(){
background(255);
for (PVector[] vecArr: lattice){
for (PVector vec : vecArr){
tile.resetMatrix();
tile.translate(vec.x, vec.y); // タイルの位置を指定
shape(tile); // タイルを描画
}
}
// 格子点を描く
for (PVector[] vecArr: lattice){
for (PVector vec : vecArr){
circle(vec.x, vec.y,10);
}
}
}