今日は、記事「五角形によるタイリング(Type 14)」を公開しました。

Type14の五角形の形状はその条件によって一意に決まります。
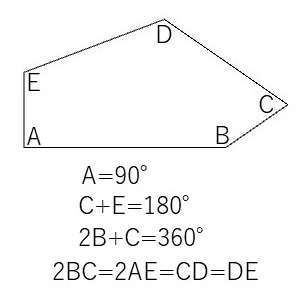
具体的には角度Cが69.32°になります。他の角度も条件式から決めることができます。辺BCの長さと辺CDの長さの比が1:2なので、角度Cが60°になるかなと直感的に期待してしまった自分がいましたが、そう単純ではなかったです。
これで一通り、15種類の五角形によるタイリングを描くことができました。
今回、15種類の五角形によるタイリングをしていて、一つ疑問が。以前再現した93種類のアイソヘドラルタイリングのうち基本図形が五角形を持つものが9種類存在していて、今回15種類の五角形によるタイリングのうち4種類が基本図形が五角形を持つアイソヘドラルタイリング9種類に属していました。では、基本図形が五角形を持つアイソヘドラルタイリング9種類のうち、残りの5種類(IH22(CM)、IH24(PMG)、IH25(PGG)、IH26(CMM)、IH29(P4G))は15種類の五角形によるタイリングのどの種類に属するのかというのが疑問です。
おそらくこれを疑問に思うのは、杉本晃久さんのサイトで紹介されている「凸五角形タイル張り問題」に記載されている『凸五角形タイル張り問題とは,タイルのTypeのファミリーを分類する問題で,タイルが作る敷きつめ模様を分類するとは違う』を理解できていないからだと思う。
タイリング問題を理解するのに、まだまだ勉強不足です。