今日は、記事「五角形によるタイリング(Type 12)」を公開しました。

Type 12の五角形を準備するとき、今回基準となる角度として\(C=60^{\circ}\)と取りました。その結果、△BCDが角度30°、60°、90°をもつ直角三角形になりました。
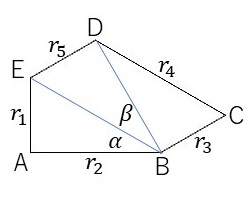
そこで、ちょっと仮説を立ててみました。
\( \angle CBE \)は角度Cの取り方によらずに90°になる?
これについて、ちょっと実験してみました。以下の図は左が\(C=50^{\circ}\)としたときの五角形、右が\(C=70^{\circ}\)としたときの五角形になります。
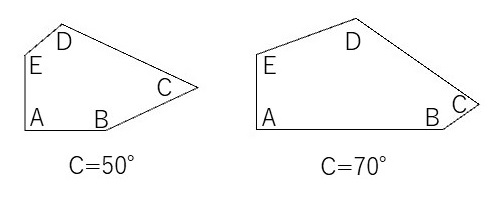
これらの図形を眺めてみると、\( \angle CBE \)は90°担っているようにも見えます。そこで実際に、\( \angle CBE \)を計算してみました。結果、\[ C=50^{\circ} \ \ \to \angle CBE = 87.52^{\circ}, \ \ C=70^{\circ} \ \ \to \angle CBE = 92.97^{\circ} \]と、微妙に90°からずれていました。というわけで、\( \angle CBE \)が90°になるのは、角度Cが60°のときだけのようです。
せっかくなので、この話は記事「五角形によるタイリング(Type 12)」に考察として残しておくことにします。