ここでは、書籍「アートで魅せる数学の世界」の「五角形によるタイリング」(p.93)を参考にして、五角形によるタイリング(Type 15)をProcessingで再現したいと思います。
Contents
五角形によるタイリング(Type 15)
今回、再現した五角形によるタイリング(Type 15)は以下のような図形になります。

このような五角形によるタイリングは現状15タイプあることが知られているそうです。今回の図形はその15番目になります。
この図形はぱっと見て脈略なく五角形が並べられているように見えると思いますが、実際はある法則をもって並べられています。これを見るために、この図形に色を付けてみます。

各五角形を6種類の色に塗り分けています。この結果から、いずれかと隣り合い、色が異なる6つの五角形の組合せを基本図形として、それをアイソヘドラルタイリングIH4(P2)の対称性をもつように並べていくことで、この図形を再現することができます。
描き方
この五角形によるタイリングの描き方について、順に解説していきます。
五角形の準備
今回利用する五角形は以下のような図形になります。
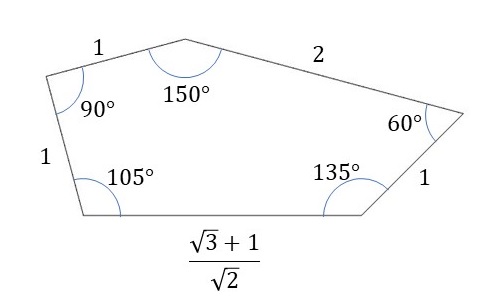
五角形の各頂点の角度から、各辺の長さの比も決まります。
基本図形の準備
次に、基本図形を準備します。先ほど、基本図形は「いずれかと隣り合い、色が異なる6つの五角形の組合せ」となることを説明しました。今回は、以下のような組合せを基本図形とします(ほかにも組合せはあります)。
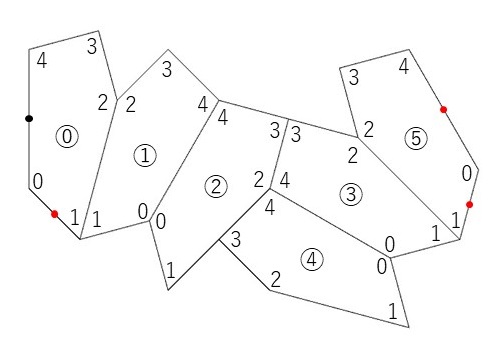
この基本図形を実際に描いていくための手順を示しておきます。
- ⓪の図形を描きます。
- ⓪の五角形の頂点1と2を結んだ直線を軸に鏡映することで①の五角形を描きます。
- ①の五角形の頂点4と0を結んだ直線を軸に鏡映することで②の五角形を描きます。
- ②の五角形の頂点3の周りで反時計回りに90度回転することで③の五角形を描きます。
- ③の五角形の頂点4と0を結んだ直線を軸に鏡映することで④の五角形を描きます。
- ③の五角形の頂点1と2を結んだ直線を軸に鏡映することで⑤の五角形を描きます。
なお、壁紙群P2の対称性に合わせて基本図形を並べていく際に、今回は⓪の五角形の頂点4と0の中点(上図の黒丸)を一般格子点と合うようにしています。また、⓪の五角形の頂点0と1の中点、⑤の五角形の頂点4と0の中点、および⑤の五角形の頂点0と1の中点(いずれも上図の赤丸)を隣り合う一般格子点同士の中点と一致するようにします。
一般格子の準備
上記で説明したように、上図の黒丸や赤丸がそれぞれ一般格子点や隣り合う一般格子点同士の中点と一致するようにとりますので、それに伴い、一般格子の形状も決まってきます。つまり、一般格子を張る2つのベクトルは、⓪の五角形の頂点4と0の中点から⑤の五角形の頂点4と0の中点へのベクトルを2倍したものと、⓪の五角形の頂点4と0の中点から⓪の五角形の頂点0と1の中点へのベクトルを2倍したものとになります。
壁紙群P2の対称性に合わせて並べる
ここまで準備ができたら、あとは壁紙群P2の対称性に合わせて基本図形を並べていくことで五角形によるタイリングを行うことができます。
ソースコード
今回再現した五角形によるタイリング(Type 15)のプログラムのソースコードを示しておきます。
PVector[][] lattice; // 格子点ベクトル
PShape tile; // タイル
float pentagon_size = 50.0; // 五角形の基準サイズ
PVector[][] v = new PVector[6][5]; // 基本図形を構成する6つの五角形の座標
PVector[] base = new PVector[2]; // 格子を張るベクトル
void setup(){
size(1000, 1000, P2D);
noFill();
makeTileP2(); // タイルを生成
makeGeneralVector(); // 一般格子を張るベクトルの生成
makeLattice(); // 格子点ベクトルを生成
drawTiling(); // タイリングを描画
}
// 五角形の頂点を取得する関数
PVector[] getPentagon(){
PVector[] v = new PVector[5];
v[0] = PVector.fromAngle(radians(90.0)).mult(pentagon_size * (sqrt(3.0) + 1.0)/sqrt(2.0)/2.0);
v[1] = v[0].copy().add( PVector.fromAngle(radians(45.0)).mult(pentagon_size));
v[2] = v[1].copy().add( PVector.fromAngle(radians(-75.0)).mult(2.0 * pentagon_size));
v[4] = PVector.fromAngle(radians(-90.0)).mult(pentagon_size * (sqrt(3.0) + 1.0)/sqrt(2.0)/2.0);
v[3] = v[4].copy().add( PVector.fromAngle(radians(-15.0)).mult(pentagon_size));
return v;
}
// 五角形を指定された軸に対して鏡映する関数
PVector[] getReflection(
PVector[] v, // 鏡映する元の図形の頂点座標
int index1, // 鏡映軸の指定するための始点位置のindex
int index2 // 鏡映軸の指定するための終点位置のindex
){
PVector[] ref = new PVector[5];
PVector axis = v[index1].copy().sub(v[index2].copy());
for(int i=0; i<5; i++){
PVector temp = v[i].copy().sub(v[index1].copy());
float t = temp.dot(axis)/ axis.dot(axis);
PVector p = v[index1].copy().add( axis.copy().mult(t) );
ref[i] = p.copy().mult(2.0).sub(v[i].copy());
}
return ref;
}
// 五角形を指定された点の周りで回転する関数
PVector[] getRotation(
PVector[] v, // 回転する元の図形の頂点座標
int index, // 回転軸の座標位置のindex
float angle // 回転角度
){
PVector[] rot = new PVector[5];
for(int i=0; i<5; i++){
PVector temp = v[i].copy().sub(v[index].copy());
PVector p = temp.copy().rotate(radians(angle));
rot[i] = v[index].copy().add(p.copy());
}
return rot;
}
// 6つの五角形から構成される基本図形を生成する関数
PShape makeFundamentalShape(){
// 6つの五角形のそれぞれの座標を取得
v[0] = getPentagon();
v[1] = getReflection(v[0], 1, 2);
v[2] = getReflection(v[1], 0, 4);
v[3] = getRotation(v[2], 3, -90.0);
v[4] = getReflection(v[3], 4, 0);
v[5] = getReflection(v[3], 1, 2);
// 五角形を6つ描いて1つのグループにまとめる
PShape pentagons = createShape(GROUP);
for(int i=0; i<6; i++){
PShape pentagon = createShape();
pentagon.beginShape();
for(int j=0; j<5; j++){
pentagon.vertex(v[i][j].x, v[i][j].y);
}
pentagon.endShape(CLOSE);
pentagons.addChild(pentagon);
}
return pentagons;
}
// タイルを生成する関数
void makeTileP2(){
tile = createShape(GROUP); // PShapeのグループを作る
for(int i=0; i<2; i++){
PShape pentagons = makeFundamentalShape(); // 6つの五角形で構成される図形の生成
pentagons.rotate(PI * i); // 180度回転
tile.addChild(pentagons); // グループに追加
}
}
// 一般格子を張るベクトルを生成する関数
// 基本図形のサイズから算出する
void makeGeneralVector(){
base[0] = v[5][0].copy().add( v[5][4].copy().sub(v[5][0].copy()).mult(0.5) ).mult(2.0);
base[1] = v[0][0].copy().add( v[0][1].copy().sub(v[0][0].copy()).mult(0.5) ).mult(2.0);
}
// 一般格子を生成する関数
void makeLattice(){
int col_num = ceil(width / base[0].x) + 1; // 列数
int row_num = ceil(height / base[1].y) + 1; // 行の数
lattice = new PVector[col_num][row_num];
for (int i = 0; i < col_num; i++){
for (int j = 0; j < row_num; j++){
PVector v = PVector.mult(base[0], i);
v.add(PVector.mult(base[1], j));
lattice[i][j] = v.copy();
}
}
}
// 格子形状に合わせたタイリングを描画する関数
void drawTiling(){
// background(255);
for (int i=0; i<lattice.length; i++){
for (int j=0; j<lattice[0].length; j++){
tile.resetMatrix();
tile.translate(lattice[i][j].x, lattice[i][j].y); // タイルの位置を指定
shape(tile); // タイルを描画
}
}
}
考察
今回解説した五角形によるタイリング(Type 15)について、その原著論文を眺めていたところ、そのp.24のFigure 10 : The Type 15 pentagon (b)にタイリングを色分けした図が載っていました。その図は、6種類の色分けではなく、以下のように3種類の色分けになっていました。

この五角形によるタイリング(Type 15)は、6つの五角形の塊ではなく、3つの五角形の塊がベースとなっていそうな気がしていましたが、原著論文ではやはりそう見ているようです。
そこで、もう一度、アイソヘドラルタイリングIH4(P2)としてみたときの基本図形を見直してみました。
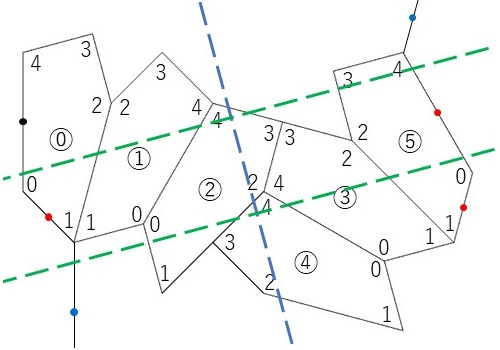
まず、3つの五角形⓪①②の組合せは3つの五角形⑤③④の組合せと合同であることはわかりますが、もう少し言えば、図の青色の点線に沿ってすべり鏡映になっていることが分かります。さらに、この図では分かりにくいですが、緑色の点線に沿ってもすべり鏡映になっています。
また、今度は以下の図のように、格子の観点でみていくとさらに面白いことが分かりました。
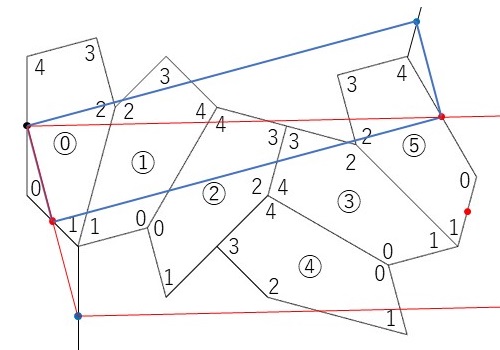
最初、赤色の線で描いているように、ベースとなる格子を一般格子としてとらえていました。そのため、アイソヘドラルタイリングIH4(P2)とみなして五角形によるタイリングを行ったわけです。今回、この格子の形状を再度見直していった結果、青色の線で描いたように格子点同士を組み合わせると、一般格子ではなく、長方格子の形状が見えてきました。
以上のことをまとめると、今回の五角形によるタイリングは3つの五角形⓪①②の組合せを基本図形とするアイソヘドラルタイリングIH5(PGG)の対称性を持つタイリングとなるようです。
実際に、アイソヘドラルタイリングIH5(PGG)として五角形によるタイリング(Type 15)を再現してみました。なお、今回は長方格子点も描いています。

また、そのプログラムのソースコードも載せておきます。
PVector[][] lattice; // 格子点ベクトル
PShape tile; // タイル
float pentagon_size = 50.0; // 五角形の基準サイズ
PVector[][] v = new PVector[6][5]; // 基本図形を構成する6つの五角形の座標
PVector[] base = new PVector[2]; // 格子を張るベクトル
void setup(){
size(1000, 1000, P2D);
noFill();
makeRectVector(); // 長方格子を張るベクトルの生成
makeTilePGG(); // タイルを生成
makeLattice(); // 格子点ベクトルを生成
drawTiling(); // タイリングを描画
}
// 五角形の頂点を取得する関数
PVector[] getPentagon(){
PVector[] v = new PVector[6];
v[0] = PVector.fromAngle(radians(90.0)).mult(pentagon_size * (sqrt(3.0) + 1.0)/sqrt(2.0)/2.0);
v[1] = v[0].copy().add( PVector.fromAngle(radians(45.0)).mult(pentagon_size));
v[2] = v[1].copy().add( PVector.fromAngle(radians(-75.0)).mult(2.0 * pentagon_size));
v[4] = PVector.fromAngle(radians(-90.0)).mult(pentagon_size * (sqrt(3.0) + 1.0)/sqrt(2.0)/2.0);
v[3] = v[4].copy().add( PVector.fromAngle(radians(-15.0)).mult(pentagon_size));
return v;
}
// 五角形を指定された軸に対して鏡映する関数
PVector[] getReflection(
PVector[] v, // 鏡映する元の図形の頂点座標
int index1, // 鏡映軸の指定するための始点位置のindex
int index2 // 鏡映軸の指定するための終点位置のindex
){
PVector[] ref = new PVector[5];
PVector axis = v[index1].copy().sub(v[index2].copy());
for(int i=0; i<5; i++){
PVector temp = v[i].copy().sub(v[index1].copy());
float t = temp.dot(axis)/ axis.dot(axis);
PVector p = v[index1].copy().add( axis.copy().mult(t) );
ref[i] = p.copy().mult(2.0).sub(v[i].copy());
}
return ref;
}
// 五角形を指定された点の周りで回転する関数
PVector[] getRotation(
PVector[] v, // 回転する元の図形の頂点座標
int index, // 回転軸の座標位置のindex
float angle // 回転角度
){
PVector[] rot = new PVector[5];
for(int i=0; i<5; i++){
PVector temp = v[i].copy().sub(v[index].copy());
PVector p = temp.copy().rotate(radians(angle));
rot[i] = v[index].copy().add(p.copy());
}
return rot;
}
// 長方格子を張るベクトルを生成する関数
// 基本図形のサイズから算出する
void makeRectVector(){
// 6つの五角形のそれぞれの座標を取得
v[0] = getPentagon();
v[1] = getReflection(v[0], 1, 2);
v[2] = getReflection(v[1], 0, 4);
v[3] = getRotation(v[2], 3, -90.0);
v[4] = getReflection(v[3], 4, 0);
v[5] = getReflection(v[3], 1, 2);
base[1] = v[0][0].copy().add( v[0][1].copy().sub(v[0][0].copy()).mult(0.5) );
base[0] = v[5][0].copy().add( v[5][4].copy().sub(v[5][0].copy()).mult(0.5) ).sub(base[1].copy());
}
// 長方格子を生成する関数
void makeLattice(){
int col_num = ceil(width / base[0].x) + 1; // 列数
int row_num = ceil(height / base[1].y) + 3; // 行の数
lattice = new PVector[col_num][row_num];
for (int i = 0; i < col_num; i++){
for (int j = 0; j < row_num; j++){
PVector v = PVector.mult(base[0], i);
v.add(PVector.mult(base[1], j));
lattice[i][j] = v.copy();
}
}
}
// 3つの五角形から構成される基本図形を生成する関数
PShape makeFundamentalShape(){
// 3つの五角形のそれぞれの座標を取得
v[0] = getPentagon();
v[1] = getReflection(v[0], 1, 2);
v[2] = getReflection(v[1], 0, 4);
// 五角形を3つ描いて1つのグループにまとめる
PShape pentagons = createShape(GROUP);
for(int i=0; i<3; i++){
PShape pentagon = createShape();
pentagon.beginShape();
for(int j=0; j<5; j++){
pentagon.vertex(v[i][j].x, v[i][j].y);
}
pentagon.endShape(CLOSE);
pentagons.addChild(pentagon);
}
return pentagons;
}
// タイルを生成する関数
void makeTilePGG(){
tile = createShape(GROUP); // PShapeのグループを作る
PShape pentagons = makeFundamentalShape(); // 3つの五角形で構成される図形の生成
tile.addChild(pentagons); // グループに追加
pentagons = makeFundamentalShape(); // 3つの五角形で構成される図形の生成
pentagons.scale(pow(-1,1),pow(-1,1)); // 六角形の反転
tile.addChild(pentagons); // グループに追加
float angle = atan2(v[5][0].y-v[5][4].y, v[5][0].x-v[5][4].x) - PI/2.0;
pentagons = makeFundamentalShape(); // 3つの五角形で構成される図形の生成
pentagons.scale(pow(-1,1),pow(-1,0)); // 六角形の反転
pentagons.rotate(angle);
pentagons.translate(base[0].x + base[1].x, base[0].y + base[1].y); // 六角形の位置を調整
tile.addChild(pentagons); // グループに追加
pentagons = makeFundamentalShape(); // 3つの五角形で構成される図形の生成
pentagons.scale(pow(-1,0),pow(-1,1)); // 六角形の反転
pentagons.rotate(angle);
pentagons.translate(-base[0].x - base[1].x, - base[0].y - base[1].y); // 六角形の位置を調整
tile.addChild(pentagons); // グループに追加
}
// 格子形状に合わせたタイリングを描画する関数
void drawTiling(){
// background(255);
for (int i=0; i<lattice.length; i++){
for (int j=0; j<lattice[0].length; j++){
if( i%2 == 0 && j%2 == 0 ){
tile.resetMatrix();
tile.translate(lattice[i][j].x, lattice[i][j].y); // タイルの位置を指定
shape(tile); // タイルを描画
}
}
}
// 格子点を描く
for (int i=0; i<lattice.length; i++){
for (int j=0; j<lattice[0].length; j++){
circle(lattice[i][j].x, lattice[i][j].y, 10);
}
}
}