ここでは、書籍「アートで魅せる数学の世界」のp.170-187で解説されている、パスカルの三角形を用いたシェルピンスキー・ギャスケット、およびデラノイの三角形を用いたシェルピンスキー・カーペットを再現してみました。
Contents
パスカルの三角形を用いたシェルピンスキー・ギャスケット
パスカルの三角形
パスカルの三角形とは、「横に並んだ2つの数の和を、その2つの数の間の下に記していく」というルールで描くことができる数の並びになります。
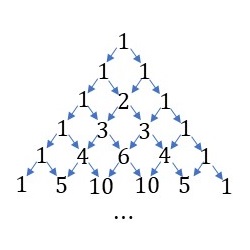
このパスカルの三角形の各数値の位置の色を、奇数の場合に白色、偶数の場合に黒色で塗っていくと、その図形はシェルピンスキー・ギャスケットになります。

ソースコード
パスカルの三角形を用いたシェルピンスキー・ギャスケットを描くためのプログラムのソースコードを示しておきます。
パスカルの三角形をどんどん深く計算していくと、数値はどんどん大きくなっていくため、int型の最大値をすぐに超えてしまいます。ただ、今回は各数値が偶数か、奇数かが知りたいので、数値を計算するたびに2で割ってそのあまりのみを保持するようにしてオーバーフローを回避しました。
void setup(){
size(512,512);
background(255,255,255);
int gasket_size = width;
int[][] gasket = new int[gasket_size][gasket_size];
for(int i=0; i<gasket_size; i++){
for(int j=0; j<gasket_size; j++){
gasket[i][j] = 0;
}
}
for(int i=0; i<gasket_size; i++){
gasket[i][0] = 1;
}
for(int j=1; j<gasket_size; j++){
gasket[0][j] = 1;
}
for(int i=2; i<gasket_size; i++){
for(int j=1; j<i; j++){
gasket[i-j][j] = (gasket[i-j-1][j] + gasket[i-j][j-1]) % 2;
}
}
for(int i=0; i<gasket_size; i++){
for(int j=0; j<gasket_size; j++){
if( gasket[i][j] == 0 ){
stroke(0,0,0);
point(i, j);
} else {
stroke(255,255,255);
point(i, j);
}
}
}
}デラノイの三角形を用いたシェルピンスキー・カーペット
デラノイの三角形
デラノイの三角形は、「横に並んだ2つの数とさらにその上の数の和を、2つの数の間の下に記していく」というルールで描くことができる数の並びになります。
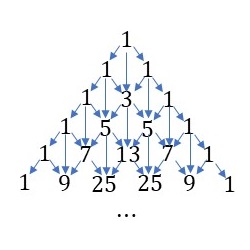
このデラノイの三角形の各数値の位置の色を、各数値をある値\(p ( \geq 3)\)で割った時の余りの値で塗り分けていくと、その図形はより一般化されたシェルピンスキー・カーペットになります。









ソースコード
デラノイの三角形を用いたシェルピンスキー・カーペットを描くためのプログラムのソースコードを示しておきます。
void setup(){
size(729,729);
background(255,255,255);
int gasket_size = width;
int p = 3;
int[][] gasket = new int[gasket_size][gasket_size];
for(int i=0; i<gasket_size; i++){
for(int j=0; j<gasket_size; j++){
gasket[i][j] = 0;
}
}
for(int i=0; i<gasket_size; i++){
gasket[i][0] = 1;
}
for(int j=1; j<gasket_size; j++){
gasket[0][j] = 1;
}
for(int i=2; i<gasket_size; i++){
for(int j=1; j<i; j++){
gasket[i-j][j] = (gasket[i-j-1][j-1] + gasket[i-j-1][j] + gasket[i-j][j-1]) % p;
}
}
for(int i=gasket_size; i<2*gasket_size; i++){
for(int j=i-gasket_size+1; j<gasket_size; j++){
gasket[i-j][j] = (gasket[i-j-1][j-1] + gasket[i-j-1][j] + gasket[i-j][j-1]) % p;
}
}
for(int i=0; i<gasket_size; i++){
for(int j=0; j<gasket_size; j++){
stroke(gasket[i][j] * 255 / (p-1), 0, 0);
point(i, j);
}
}
}