ここでは、書籍「アートで魅せる数学の世界」のp.213-226に掲載されている、ストレンジアトラクターを再現してみました。
Contents
クリフォード・アトラクター
今回描いたクリフォード・アトラクターです。

クリフォード・アトラクターの非線形方程式
クリフォード・アトラクターを描くための非線形方程式は以下となります。\[ x \to \sin (a y)+c \cos (a x), \ \ y \to \sin (b x)+d \cos (b y) \]
プログラムコード
今回作成したクリフォード・アトラクターのプログラムコードを示します。なお、クリフォード・アトラクターの各パラメータは\(a=-1.7, \ \ b=-1.8, \ \ c=-2.3, \ \ d=-0.3\)にとっています。また、最初の座標を\((0.1,0.1)\)とし、反復回数を240000回にしています。
// クリフォード・アトラクター
int iteration_num = 240000; // 反復回数
void setup(){
size(600,600);
background(0,0,0);
translate(width/2.0,height/2.0);
stroke(255,255,255);
strokeWeight(0.1);
// 図形のサイズを調整
float x_scale = width/8.0;
float y_scale = height/8.0;
// クリフォード・アトラクターのパラメータ
float a = -1.7;
float b = -1.8;
float c = -2.3;
float d = -0.3;
// クリフォード・アトラクターを描画
float x = 0.1;
float y = 0.1;
float next_x, next_y;
point(x*x_scale, -y*y_scale);
int iter = 0;
while(iter<iteration_num){
next_x = sin(a*y) + c*cos(a*x);
next_y = sin(b*x) + d*cos(b*y);
x = next_x;
y = next_y;
point(x*x_scale, -y*y_scale);
iter++;
}
}デヨン・アトラクター
今回描いたデヨン・アトラクターです。これは、別記事「非線型変換を含むフラクタル」で紹介した「デ・ヨング・アトラクター」と同じもので、パラメータの値が変わったものです。

デヨン・アトラクターの非線形方程式
デヨン・アトラクターを描くための非線形方程式は以下となります。\[ x \to \sin (a y) – \cos (b x), \ \ y \to \sin (c x)- \cos (d y) \]
プログラムコード
今回作成したデヨン・アトラクターのプログラムコードを示します。なお、デヨン・アトラクターの各パラメータは\(a=-2, \ \ b=-2.3, \ \ c=-1.4, \ \ d=2.1\)にとっています。また、最初の座標を\((0.1,0.1)\)とし、反復回数を240000回にしています。
// デヨン・アトラクター
int iteration_num = 240000; // 反復回数
void setup(){
size(600,600);
background(0,0,0);
translate(width/2.0,height/2.0);
stroke(255,255,255);
strokeWeight(0.1);
// 図形のサイズを調整
float x_scale = width/5.0;
float y_scale = height/5.0;
// デヨン・アトラクターのパラメータ
float a = -2.0;
float b = -2.3;
float c = -1.4;
float d = 2.1;
// デヨン・アトラクターを描画
float x = 0.1;
float y = 0.1;
float next_x, next_y;
point(x*x_scale, -y*y_scale);
int iter = 0;
while(iter<iteration_num){
next_x = sin(a*y)-cos(b*x);
next_y = sin(c*x)-cos(d*y);
x = next_x;
y = next_y;
point(x*x_scale, -y*y_scale);
iter++;
}
}ホパロン・アトラクター
今回描いたホパロン・アトラクターです。これは、別記事「非線型変換を含むフラクタル」で紹介した「古典的なバリー・マーティンのアトラクター」と同じもので、パラメータの値が変わったものです。

ホパロン・アトラクターの非線形方程式
ホパロン・アトラクターを描くための非線形方程式は以下となります。\[ x \to y-1-\frac{(x-1) \sqrt{|bx-1-c|}}{|x-1|}, \ \ y \to a-x-1 \]
プログラムコード
今回作成したホパロン・アトラクターのプログラムコードを示します。なお、ホパロン・アトラクターの各パラメータは\(a=9.3, \ \ b=5.78, \ \ c=7.21\)にとっています。また、最初の座標を\((0,0)\)とし、反復回数を240000回にしています。
// ホパロン・アトラクター
int iteration_num = 240000; // 反復回数
void setup(){
size(600,600);
background(0,0,0);
translate(width/2.0,height/2.0);
stroke(255,255,255);
strokeWeight(0.5);
// 図形のサイズを調整
float x_scale = width/200.0;
float y_scale = height/200.0;
// ホパロン・アトラクターのパラメータ
float a = 9.3;
float b = 5.78;
float c = 7.21;
// ホパロン・アトラクターを描画
float x = 0.0;
float y = 0.0;
float next_x, next_y;
point(x*x_scale, -y*y_scale);
int iter = 0;
while(iter<iteration_num){
next_x = y-1.0 - (x-1.0)*sqrt(abs(b*x-1.0-c))/abs(x-1.0);
next_y = a-x-1.0;
x = next_x;
y = next_y;
point(x*x_scale, -y*y_scale);
iter++;
}
}グモウスキー・ミラ・アトラクター
今回描いたグモウスキー・ミラ・アトラクターです。

グモウスキー・ミラ・アトラクターの非線形方程式
グモウスキー・ミラ・アトラクターを描くための非線形方程式は以下となります。\[ x_{n+1} = y_n + a y_n (1-by_n^2)+cx_n+ \frac{2(1-c)x_n^2}{1+x_n^2}, \ \ y_{n+1} = – x_n + cx_{n+1}+\frac{2(1-c)x_{n+1}^2}{1+x_{n+1}^2} \]
プログラムコード
今回作成したグモウスキー・ミラ・アトラクターのプログラムコードを示します。なお、グモウスキー・ミラ・アトラクターの各パラメータは\(a=0.007, \ \ b=0.05, \ \ c=-0.47\)にとっています。また、最初の座標を\((0.1,0.1)\)とし、反復回数を240000回にしています。
// グモウスキー・ミラ・アトラクター
int iteration_num = 240000; // 反復回数
void setup(){
size(600,600);
background(0,0,0);
translate(width/2.0,height/2.0);
stroke(255,255,255);
strokeWeight(0.5);
// 図形のサイズを調整
float x_scale = width/30.0;
float y_scale = height/30.0;
// グモウスキー・ミラ・アトラクターのパラメータ
float a = 0.007;
float b = 0.05;
float c = -0.47;
// グモウスキー・ミラ・アトラクターを描画
float x = 0.1;
float y = 0.1;
float next_x, next_y;
point(x*x_scale, -y*y_scale);
int iter = 0;
while(iter<iteration_num){
next_x = y+a*y*(1.0-b*y*y)+c*x+2.0*(1.0-c)*x*x/(1.0+x*x);
next_y = -x+c*next_x+2.0*(1.0-c)*next_x*next_x/(1.0+next_x*next_x);
x = next_x;
y = next_y;
point(x*x_scale, -y*y_scale);
iter++;
}
}池田アトラクター
今回描いた池田アトラクターです。

池田アトラクターの非線形方程式
池田アトラクターを描くための非線形方程式は以下となります。\[ u \to 0.4 – \frac{6}{1+x^2+y^2}, \\ x \to 1+a(x \cos u – y \sin u), \ \ y \to a(x \sin u + y \cos u) \]
プログラムコード
今回作成した池田アトラクターのプログラムコードを示します。なお、池田アトラクターの各パラメータは\(a=0.901\)にとっています。また、最初の座標を\((0.1,0.1)\)とし、反復回数を240000回にしています。
// 池田アトラクター
int iteration_num = 240000; // 反復回数
void setup(){
size(600,600);
background(0,0,0);
translate(width/3.0,height/3.0);
stroke(255,255,255);
strokeWeight(0.5);
// 図形のサイズを調整
float x_scale = width/4.0;
float y_scale = height/4.0;
// 池田アトラクターのパラメータ
float a = 0.901;
// 池田アトラクターを描画
float x = 0.1;
float y = 0.1;
float u = 0.0;
float next_x, next_y;
point(x*x_scale, -y*y_scale);
int iter = 0;
while(iter<iteration_num){
u = 0.4-6.0/(1.0+x*x+y*y);
next_x = 1.0+a*(x*cos(u)-y*sin(u));
next_y = a*(x*sin(u)+y*cos(u));
x = next_x;
y = next_y;
point(x*x_scale, -y*y_scale);
iter++;
}
}Goldfish
今回描いたGoldfishです。

Goldfishの非線形方程式
Goldfishを描くための非線形方程式は以下となります。\[ x \to \cos (ax-y)+y \sin(bxy), \ \ y \to x + b \sin y \]
プログラムコード
今回作成したGoldfishのプログラムコードを示します。なお、Goldfishの各パラメータは\(a=-0.64, \ \ b=1.25 \)にとっています。また、最初の座標を\((1,1)\)とし、反復回数を300000回にしています。
// Goldfish
int iteration_num = 300000; // 反復回数
void setup(){
size(600,600);
background(0,0,0);
translate(width/2.0,height*3.0/5.0);
stroke(255,255,0);
strokeWeight(0.5);
// 図形のサイズを調整
float x_scale = width/5.0;
float y_scale = height/5.0;
// Goldfishのパラメータ
float a = -0.64;
float b = 1.25;
// Goldfishを描画
float x = 1.0;
float y = 1.0;
float next_x, next_y;
point(x*x_scale, -y*y_scale);
int iter = 0;
while(iter<iteration_num){
next_x = cos(a*x-y)+y*sin(b*x*y);
next_y = x+b*sin(y);
x = next_x;
y = next_y;
point(x*x_scale, -y*y_scale);
iter++;
}
}Rebirth
今回描いたRebirthです。
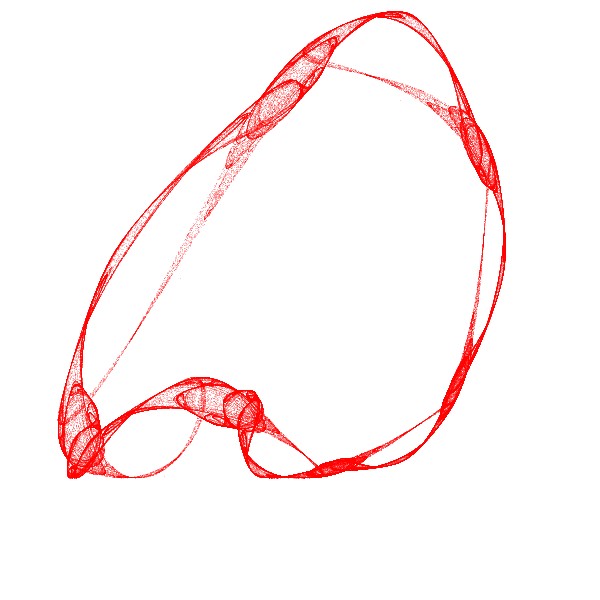
Rebirthの非線形方程式
Rebirthを描くための非線形方程式は以下となります。\[ x \to ax+by, \ \ y \to x^2 + b \]
プログラムコード
今回作成したRebirthのプログラムコードを示します。なお、Rebirthの各パラメータは\(a=0.79, \ \ b=-0.89 \)にとっています。また、最初の座標を\((1,1)\)とし、反復回数を300000回にしています。
// Rebirth
int iteration_num = 300000; // 反復回数
void setup(){
size(600,600);
background(255,255,255);
translate(width/3.0,height/2.0);
stroke(255,0,0);
strokeWeight(0.5);
// 図形のサイズを調整
float x_scale = width/3.0;
float y_scale = height/3.0;
// Rebirthのパラメータ
float a = 0.79;
float b = -0.89;
// Rebirthを描画
float x = 1.0;
float y = 1.0;
float next_x, next_y;
point(x*x_scale, -y*y_scale);
int iter = 0;
while(iter<iteration_num){
next_x = a*x+b*y;
next_y = x*x+b;
x = next_x;
y = next_y;
point(x*x_scale, -y*y_scale);
iter++;
}
}Chaotic Cylinder
今回描いたChaotic Cylinderです。
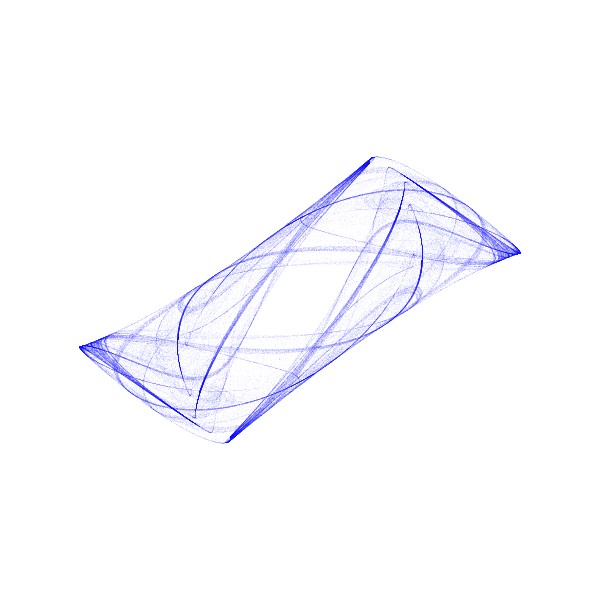
Chaotic Cylinderの非線形方程式
Chaotic Cylinderを描くための非線形方程式は以下となります。\[ x \to x+a \sin ( 2 \pi y ), \ \ y \to x \cos (2 \pi y ) + ay \]
プログラムコード
今回作成したChaotic Cylinderのプログラムコードを示します。なお、Chaotic Cylinderの各パラメータは\(a=-0.56 \)にとっています。また、最初の座標を\((0.1,0.1)\)とし、反復回数を300000回にしています。
// Chaotic Cylinder
int iteration_num = 300000; // 反復回数
void setup(){
size(600,600);
background(255,255,255);
translate(width/2.0,height/2.0);
stroke(0,0,255);
strokeWeight(0.1);
// 図形のサイズを調整
float x_scale = width*2.0/3.0;
float y_scale = height*2.0/3.0;
// Chaotic Cylinderのパラメータ
float a = -0.56;
// Chaotic Cylinderを描画
float x = 0.1;
float y = 0.1;
float next_x, next_y;
point(x*x_scale, -y*y_scale);
int iter = 0;
while(iter<iteration_num){
next_x = x+a*sin(2.0 * PI * y);
next_y = x*cos(2.0 * PI * y)+a*y;
x = next_x;
y = next_y;
point(x*x_scale, -y*y_scale);
iter++;
}
}