ここでは、\(N=2\)以上のリサージュ図形において、振幅の大きさが大きな軌道(主軌道と呼ぶことにします)に、振幅の大きさが小さくて周波数が主軌道よりも大きい軌道(副軌道と呼ぶことにします)を加えるとき、副軌道のリサージュ曲線を主軌道に対して垂直に交わるように回転することを考えます。
副軌道の回転について
記事「トーラス型コイル」では、主軌道となる円の周りを螺旋状に副軌道となる楕円が巻き付いていくようなリサージュ図形を描きました。その際、副軌道となる楕円を主軌道と垂直に交わるように回転をしました。ここでは、より一般的に、副軌道となる楕円を主軌道と垂直に交わるように回転することについて考えていきます。
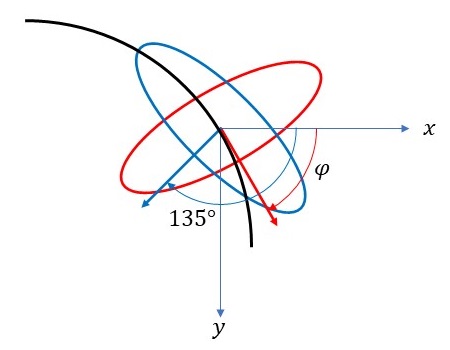
上記の図において、黒色の曲線は主軌道を表し、青色と赤色の楕円は副軌道を表しています。記事「リサージュ図形(N=1)」の「位相を変化させる」のところでみたように、リサージュ曲線で描かれる楕円は基本的に45°傾いた形(青色の楕円)をしていることが反映されています。ここでは、この青色の楕円を赤色の楕円のように、主軌道に垂直になるように回転することを考えます。
青色の楕円は基本的に45°傾いた形をしているので、この楕円に垂直なベクトル(青色の矢印)は\(x\)軸の正の向きから常に135°回転した方向に向いています。ここでは、この青色の楕円を赤色の楕円のように主軌道(黒色の曲線)に垂直になるように回転することを考えています。これは、青色の矢印が主軌道の接線方向(赤色の矢印)に一致するように回転させることで実現できます。つまり、主軌道の接線方向(赤色の矢印)が\(x\)軸の正の向きから\( \varphi \)だけ傾いているとすると、青色の楕円上のすべての点を\( \varphi−135 \)度だけ回転させることで、青色の楕円を赤色の楕円のように主軌道に垂直にすることができます。
次に、\( \varphi \)を求めてみます。主軌道上の座標を\( (x(t),y(t)) \)とすると、主軌道の接線方向(赤色の矢印)は、主軌道上の座標をパラメータ\(t\)で微分した\( (x'(t), y'(t)) \)で表されます。この接線のベクトルから\[ \varphi (t) = \arctan \left( \frac{y'(t)}{x'(t)} \right) \]で\( \varphi(t) \)を求めることができます。
あとは、副軌道となる青色の楕円上の点を座標\( ( r \cos \omega t , r \sin (\omega t + \theta ) ) \)で表すと、楕円上の点を楕円の中心回りに時計回りに\( \varphi (t) -135 \)だけ回転させるには、\[ \begin{pmatrix} \cos ( \varphi (t) -135 ) & -\sin ( \varphi (t) -135 ) \\ \sin ( \varphi (t) -135 ) & \cos ( \varphi (t) -135 ) \end{pmatrix} \begin{pmatrix} r \cos \omega t \\ r \sin (\omega t + \theta ) \end{pmatrix} = \begin{pmatrix} r \cos \omega t \cos ( \varphi (t) -135 ) – r \sin ( \omega t + \theta ) \sin ( \varphi (t) -135 ) \\ r \cos \omega t \sin ( \varphi (t) -135 ) + r \sin (\omega t + \theta ) \cos ( \varphi (t) -135 ) \end{pmatrix} \]のように座標変換することで実現することができますので、これを主軌道の座標\( (x(t),y(t)) \)に加えることで、副軌道が主軌道と垂直に交わるような図形を描くことができます。
この副軌道の回転はリサージュ図形なのか
上記で主軌道の接線ベクトルから回転角度\( \varphi(t) \)を求めました。
記事「トーラス型コイル」では、主軌道が円であったため\( \varphi(t) \)は\( \Omega t + 90 \)のようにパラメータ\(t\)に対して線形の形をしていました。そのため、上記の座標変換の右辺の式は\(\sin, \cos \)の加法定理を用いて\( \sin, \cos \)の和に分解すると、結果として\(N=4\)のリサージュ図形の形で表現することができました。
一方、任意の形の主軌道に対して\( \varphi(t) \)は一般に非線形の形になります。そのため、上記の座標変換の右辺の式を\(\sin, \cos \)の加法定理を用いて\( \sin, \cos \)の和に分解しても、それぞれの\( \sin, \cos \)の引数がパラメータ\(t\)の非線形関数で表されることになり、結果としてリサージュ図形とは呼べないものになってしまいます。
とはいえ、これも「拡張された」リサージュ図形として考えてもいいかもしれません。