よく新聞などで見かける、絵の中に立体が浮かび上がるアート。ここでは、このような画像の中にステレオグラムを埋め込む方法について解説していきたいと思います。
一見難しそうですが、ステレオグラムの原理は記事「ランダムドット・ステレオグラム」で解説したものと同じものですので、比較的簡単に理解できるのではないかと思います。
Contents
背景画像
今回、背景画像の例として以下の2つの画像を選びました。いずれも「photo AC」(https://photo-ac.com)の素材を利用させていただいています。


画像の中にステレオグラムを埋め込む
今回作成した画像の中にステレオグラムを埋め込んだ例を示します。


いずれも、記事「四角と丸」で紹介した立体図形が埋め込まれています。

右の「草むらの中に」埋め込んだ場合は立体視しなくても円が見えていますが、左の「模様の中に」埋め込んだ場合は、ほぼわからないのではないでしょうか。つまり、画像の中にステレオグラムを埋め込むとき、埋め込み先の画像の選択は大事になってきます。
まずシンプルに埋め込んでみる
ここから、画像の中にステレオグラムを埋め込んでいく方法について解説していきます。
ステレオグラムを埋め込む方法は基本的に記事「ランダムドット・ステレオグラム」で解説した原理と同じものを利用します。ここで、ランダムドット・ステレオグラムのときのプロットする点の位置の計算方法を復習しておきます。
紙上にプロットする点の位置の計算手順(復習)
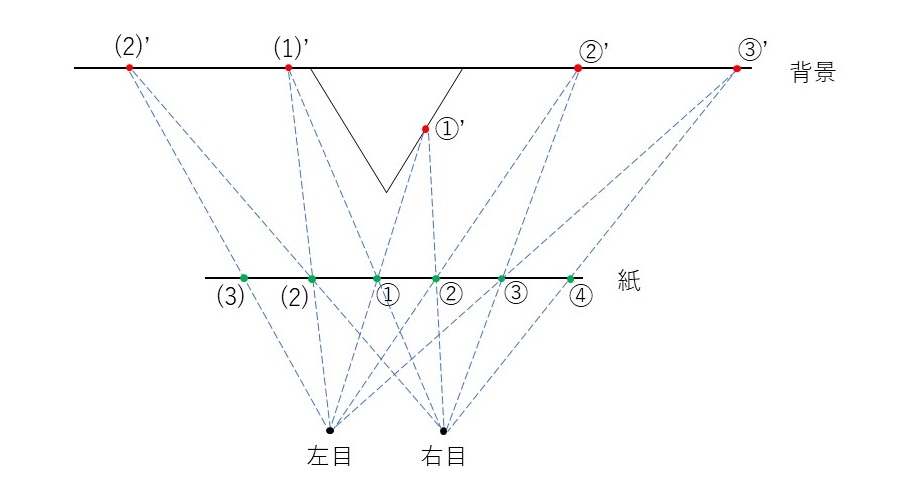
- どんな立体を見るのかを決め、関数または他の方法でその立体のデータ(情報)を与える。
- 紙上の範囲にひとつの点をランダムに描き、①として左目用の点とする。
- 左目の位置と①の点の延長線上に立体との交点①’を求め、①’を右目で見たときの紙上の点②を求め、点を描く。
- 点②を左目用の点とみなし、3を実行する。この処理を点が紙上から外れるまで繰り返し行う。
- 今度は2の①を右目用として、右目の位置と①の点の延長線上に立体との交点(1)’を求め、(1)’を左目で見たときの紙上の点(2)を求め、点を描く。
- 点(2)を右目用の点とみなし、5を実行する。この処理を点が紙上から外れるまで繰り返し行う。
- 2から6までの処理を好きなだけ繰り返す。
ランダムドット・ステレオグラムでは、紙上の点をランダムに選んでその点を起点に紙上にプロットする点の位置を計算していきました。画像の中に埋め込む場合は画像上のすべての点(つまり画素)を順に選択し、それを起点にして紙上にプロットする点の位置を計算していきます。ただし、一度プロットされた画素への上書きは禁止します。また、選択する画素の順番は、紙の縦方向の中心線から左右の方向に拡がっていくように選んでいきます。

実際に、画像上のすべての点を対象にして紙上の位置を計算してプロットしていった結果、以下の図のようになります。


この記事の最初に紹介した画像の中にステレオグラムを埋め込んだ例とほとんど同じに見えると思います。また、実際に立体視してみても、比較的きれいに立体が浮かび上がるのではないでしょうか。
ですのでこのままでもよいのですが、ちょっと気になる点があります。それは、上記の右図の草むらの図の左側に顕著に表れていますが、かすれのようなものが出ていることです。実際に、立体視してみても、このあたりの部分はちかちかして見えると思います。
以下では、その原因と、今回対処した方法について解説します。
かすれとかくれ
ステレオグラムを埋め込んだ画像は、その紙上にプロットする点の位置の計算方法からもわかるように、横方向に繰り返し同じような画像が描かれていきます。そこで、ここでは画像上のすべての画素に対して計算するのではなく、この繰り返しパターンの1ブロックの分だけ紙上にプロットする点の位置を計算してプロットすることを考えてみます。その結果、以下のような一部が欠けた画像が得られます。


この欠けた部分の原因はかすれとかくれの2種類に分かれます。
かすれ
一つ目は画像の左側に白い縦線が何本か現れているものです。これをかすれと呼んでいます。
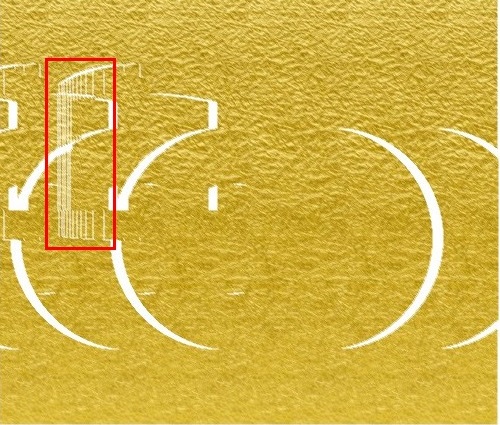
このかすれの原因は、以下のような図にすると分かりやすいと思います。
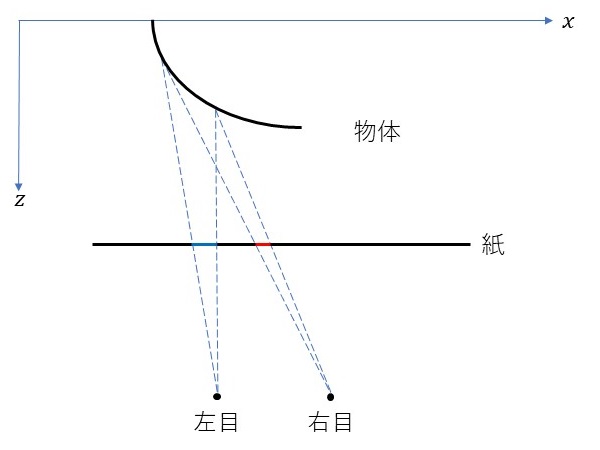
例えば、紙上の画素1ピクセル分の領域(赤色の領域)を右目から見るとします。その対応する物体の領域が左側の方向に傾いていた場合(今回の場合アーチ型をした「四角」の左側の領域に対応)、左目で同じ領域をみると、紙上に射影される領域は右目で見たときの紙上の画素1ピクセル分の領域よりも広くなります(青色の領域)。つまり、右目で見た紙上の点から対応する左目でみた点を単純に算出してその位置に同じ色をプロットするだけでは、本来の左目の領域をカバーすることができないため、白い部分(色が塗られない部分)がでてしまいます。
今回このかすれへの対処は、右目でみた紙上の点(赤色の領域)の色が左目でみた紙上の領域(青色の領域)に含まれる画素すべてに同じ色が入るようにしました。結果は以下の通りです。


かくれ
もう一つは対象となる物体の縁に現れてる白い領域です。これをかくれと呼んでいます。
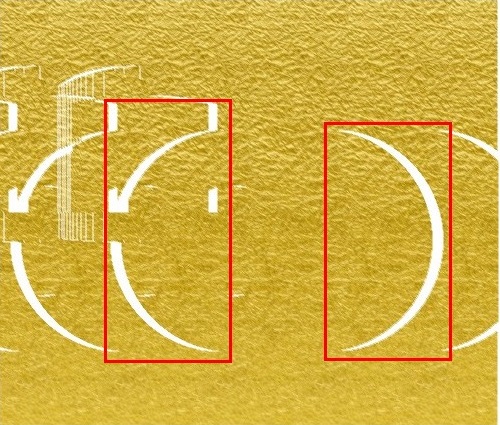
この原因は左目または右目からのどちらかから物体の影に隠れて見えなくなってしまう領域が存在することです。
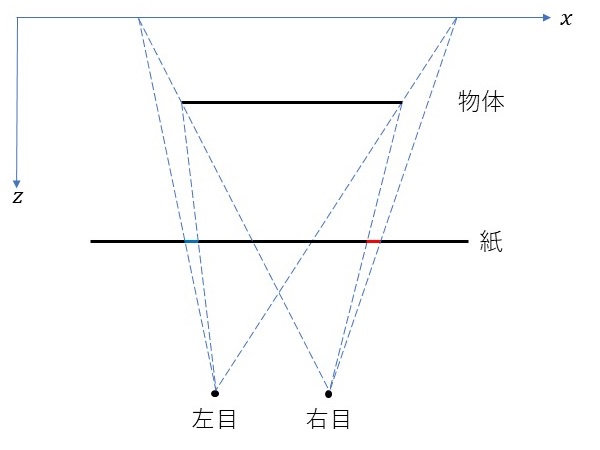
上図で、紙上の赤色の領域は右目からは見えますが、左目からは物体に遮られて見えなくなっています。同様に、紙上の青色の領域は左目からは見えますが、右目からは物体に遮られて見えなくなっています。このような紙上の領域が白色の領域として現れています。
今回、この領域については特に対処しておらず、背景の画像を単純に拾ってきています。というのも、立体視をする分には特に影響はないからです。ただ、選ぶ背景画像によっては画像が不自然な模様になってしまうので、もう少し工夫をしてもいいかもしれません。
ソースコード
今回作成したプログラムのソースコードを最後に示しておきます。なお、今回はあまり整理せずに載せました。関数化、クラス化するなどを実施したり、かすれとかくれを同時に処理したりすれば、もう少しコードも短く書けると思います。
PImage im;
int loc;
float r, g, b;
float k = 500.0; // 座標原点から紙までの距離
float m = 500.0; // 紙から目までの距離
float h = 100.0; // 目と目の間の距離の半分
float radius = 150.0; // 円の半径
float circle_pos_z = 100.0; // 円のz軸方向の位置
void setup(){
size(500,600,P2D);
background(255,255,255);
PVector point3d, point3d_rev; // 立体視したい図形上の点
float x_r, x_l, y_eye; // 紙上の点
float triangular_pyramid_size = 50.0; // 三角錐のサイズ
// 三角錐の4つの頂点のベクトル
PVector triangular_pyramid[] = new PVector[4];
triangular_pyramid[0] = new PVector(0.0, 0.0, sqrt(2.0/3.0)*triangular_pyramid_size);
triangular_pyramid[1] = new PVector(0.0, -1.0/sqrt(3.0)*triangular_pyramid_size, 0.0);
triangular_pyramid[2] = triangular_pyramid[1].copy().rotate(radians(120));
triangular_pyramid[3] = triangular_pyramid[1].copy().rotate(radians(240));
// 三角錐の位置
translate(width/2, 50);
// 紙の上に三角錐を左目用と右目用にそれぞれ射影する
for(int i=0; i<4; i++){
for(int j=i+1; j<4; j++){
for(int d=0; d<100; d++){
point3d = triangular_pyramid[i].copy().add(triangular_pyramid[j].copy().sub(triangular_pyramid[i].copy()).mult(d/100.0));
x_r = (m * point3d.x - h * point3d.z + h*k) / (m + k - point3d.z);
x_l = (m * point3d.x + h * point3d.z - h*k) / (m + k - point3d.z);
y_eye = m * point3d.y / (m + k - point3d.z);
point(x_r, y_eye);
point(x_l, y_eye);
}
}
}
// ステレオグラムを描く位置
translate(0, 300);
// 背景となる画像の読み込み
im = loadImage("Pattern.jpg");
im.loadPixels();
Integer[] flags = new Integer[width];
Integer[] color_index = new Integer[width];
float x_ini, y_ini;
// 対称物体をステレオグラム化
for(int j=0; j<im.height; j++){
y_ini = j-im.height/2; // 紙上の点の初期値y座標
// flagsを初期化
for(int l=0; l<width; l++){
flags[l]=0;
}
// 画像右側にある画素に対して処理する
for(int i=width/2; i<width; i++){
loc = i + j * im.width;
r = red(im.pixels[loc]);
g = green(im.pixels[loc]);
b = blue(im.pixels[loc]);
stroke(r, g, b);
x_ini = i-width/2; // 紙上の点の初期値x座標
// まず初期値が左目からの座標として処理する
x_l = x_ini;
y_eye = y_ini;
if(flags[symRound(x_l) + width/2] == 0){
point(symRound(x_l), symRound(y_eye));
flags[symRound(x_l) + width/2] = 1;
color_index[symRound(x_l) + width/2] = loc;
} else {
break;
}
while(true){
// この左目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_l, y_eye, -h);
// この対称物体上の点に対応する、右目からの紙上の座標位置を算出する。
x_r = (m * point3d.x - h * point3d.z + h * k) / (m + k - point3d.z);
if( abs(x_r) < width/2.0-1){
if(flags[symRound(x_r) + width/2] == 0){
point(symRound(x_r), symRound(y_eye));
flags[symRound(x_r) + width/2] = 1;
color_index[symRound(x_r) + width/2] = loc;
}
x_l = x_r;
} else {
break;
}
}
// 次に初期値を右目からの座標として処理する
x_r = x_ini;
while(true){
// この右目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_r, y_eye, h);
// この対称物体上の点に対応する、左目からの紙上の座標位置を算出する。
x_l = (m * point3d.x + h * point3d.z - h * k) / (m + k - point3d.z);
if( abs(x_l) < width/2.0){
if(flags[symRound(x_l) + width/2] == 0){
point(symRound(x_l), symRound(y_eye));
flags[symRound(x_l) + width/2] = 1;
color_index[symRound(x_l) + width/2] = loc;
}
x_r = x_l;
} else {
break;
}
}
}
// 画像左側にある画素に対して処理する
for(int i=width/2-1; i>=0; i--){
loc = i + j * im.width;
r = red(im.pixels[loc]);
g = green(im.pixels[loc]);
b = blue(im.pixels[loc]);
stroke(r, g, b);
x_ini = i-width/2; // 紙上の点の初期値x座標
// まず初期値が左目からの座標として処理する
x_l = x_ini;
y_eye = y_ini;
if(flags[symRound(x_l) + width/2] == 0){
point(symRound(x_l), symRound(y_eye));
flags[symRound(x_l) + width/2] = 1;
color_index[symRound(x_l) + width/2] = loc;
} else {
break;
}
while(true){
// この左目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_l, y_eye, -h);
// この対称物体上の点に対応する、右目からの紙上の座標位置を算出する。
x_r = (m * point3d.x - h * point3d.z + h * k) / (m + k - point3d.z);
if( abs(x_r) < width/2.0-1){
if(flags[symRound(x_r) + width/2] == 0){
point(symRound(x_r), symRound(y_eye));
flags[symRound(x_r) + width/2] = 1;
color_index[symRound(x_r) + width/2] = loc;
}
x_l = x_r;
} else {
break;
}
}
// 次に初期値を右目からの座標として処理する
x_r = x_ini;
while(true){
// この右目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_r, y_eye, h);
// この対称物体上の点に対応する、左目からの紙上の座標位置を算出する。
x_l = (m * point3d.x + h * point3d.z - h * k) / (m + k - point3d.z);
if( abs(x_l) < width/2.0){
if(flags[symRound(x_l) + width/2] == 0){
point(symRound(x_l), symRound(y_eye));
flags[symRound(x_l) + width/2] = 1;
color_index[symRound(x_l) + width/2] = loc;
}
x_r = x_l;
} else {
break;
}
}
}
// かすれへの対応
for(int i=width/2; i<width; i++){
if(flags[i] == 0){
x_r = i - width/2;
y_eye = y_ini;
// この右目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_r, y_eye, h);
// この対称物体上の点に対応する、左目からの紙上の座標位置を算出する。
x_l = (m * point3d.x + h * point3d.z - h * k) / (m + k - point3d.z);
// 算出した左目からの紙上の座標位置から改めて対称物体の上の点の位置を算出する。
point3d_rev = get3DPoint(x_l, y_eye, -h);
// point3dとpoint3d_revが一致かつpoinrt3d.z>0であれば、一つ手前の画素と同じ色でプロットするを1にする
if( abs(point3d.x - point3d_rev.x) < 0.01 && abs(point3d.z - point3d_rev.z) < 0.01 && point3d.z > 0.0 ){
loc = color_index[i-1];
r = red(im.pixels[loc]);
g = green(im.pixels[loc]);
b = blue(im.pixels[loc]);
stroke(r, g, b);
point(i-width/2, symRound(y_ini));
flags[i] = 1;
color_index[i] = loc;
x_l = i - width/2;
while(true){
// この左目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_l, y_eye, -h);
// この対称物体上の点に対応する、右目からの紙上の座標位置を算出する。
x_r = (m * point3d.x - h * point3d.z + h * k) / (m + k - point3d.z);
if( abs(x_r) < width/2.0-1){
if(flags[symRound(x_r) + width/2] == 0){
point(symRound(x_r), symRound(y_eye));
flags[symRound(x_r) + width/2] = 1;
color_index[symRound(x_r) + width/2] = loc;
}
x_l = x_r;
} else {
break;
}
}
}
}
}
for(int i=width/2-1; i>=0; i--){
if(flags[i] == 0){
x_l = i - width/2;
y_eye = y_ini;
// この右目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_l, y_eye, -h);
// この対称物体上の点に対応する、左目からの紙上の座標位置を算出する。
x_r = (m * point3d.x - h * point3d.z + h * k) / (m + k - point3d.z);
// 算出した左目からの紙上の座標位置から改めて対称物体の上の点の位置を算出する。
point3d_rev = get3DPoint(x_r, y_eye, h);
// point3dとpoint3d_revが一致かつpoinrt3d.z>0であれば、一つ手前の画素と同じ色でプロットするを1にする
if( abs(point3d.x - point3d_rev.x) < 0.001 && abs(point3d.z - point3d_rev.z) < 0.001 && point3d.z > 0.0 ){
loc = color_index[i+1];
r = red(im.pixels[loc]);
g = green(im.pixels[loc]);
b = blue(im.pixels[loc]);
stroke(r, g, b);
point(i-width/2, symRound(y_ini));
flags[i] = 1;
color_index[i] = loc;
x_r = i - width/2;
while(true){
// この右目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_r, y_eye, h);
// この対称物体上の点に対応する、左目からの紙上の座標位置を算出する。
x_l = (m * point3d.x + h * point3d.z - h * k) / (m + k - point3d.z);
if( abs(x_l) < width/2.0){
if(flags[symRound(x_l) + width/2] == 0){
point(symRound(x_l), symRound(y_eye));
flags[symRound(x_l) + width/2] = 1;
color_index[symRound(x_l) + width/2] = loc;
}
x_r = x_l;
} else {
break;
}
}
}
}
}
// かくれへの対応
for(int i=width/2; i<width; i++){
if(flags[i] == 0){
loc = i + j * im.width;
r = red(im.pixels[loc]);
g = green(im.pixels[loc]);
b = blue(im.pixels[loc]);
stroke(r, g, b);
x_ini = i-width/2; // 紙上の点の初期値x座標
// まず初期値が左目からの座標として処理する
x_l = x_ini;
y_eye = y_ini;
if(flags[symRound(x_l) + width/2] == 0){
point(symRound(x_l), symRound(y_eye));
flags[symRound(x_l) + width/2] = 1;
color_index[symRound(x_l) + width/2] = loc;
}
while(true){
// この左目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_l, y_eye, -h);
// この対称物体上の点に対応する、右目からの紙上の座標位置を算出する。
x_r = (m * point3d.x - h * point3d.z + h * k) / (m + k - point3d.z);
if( abs(x_r) < width/2.0-1){
if(flags[symRound(x_r) + width/2] == 0){
point(symRound(x_r), symRound(y_eye));
flags[symRound(x_r) + width/2] = 1;
color_index[symRound(x_r) + width/2] = loc;
}
x_l = x_r;
} else {
break;
}
}
// 次に初期値を右目からの座標として処理する
x_r = x_ini;
while(true){
// この右目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_r, y_eye, h);
// この対称物体上の点に対応する、左目からの紙上の座標位置を算出する。
x_l = (m * point3d.x + h * point3d.z - h * k) / (m + k - point3d.z);
if( abs(x_l) < width/2.0){
if(flags[symRound(x_l) + width/2] == 0){
point(symRound(x_l), symRound(y_eye));
flags[symRound(x_l) + width/2] = 1;
color_index[symRound(x_l) + width/2] = loc;
}
x_r = x_l;
} else {
break;
}
}
}
}
for(int i=width/2-1; i>=0; i--){
if(flags[i] == 0){
loc = i + j * im.width;
r = red(im.pixels[loc]);
g = green(im.pixels[loc]);
b = blue(im.pixels[loc]);
stroke(r, g, b);
x_ini = i-width/2; // 紙上の点の初期値x座標
// まず初期値が左目からの座標として処理する
x_l = x_ini;
y_eye = y_ini;
if(flags[symRound(x_l) + width/2] == 0){
point(symRound(x_l), symRound(y_eye));
flags[symRound(x_l) + width/2] = 1;
color_index[symRound(x_l) + width/2] = loc;
}
while(true){
// この左目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_l, y_eye, -h);
// この対称物体上の点に対応する、右目からの紙上の座標位置を算出する。
x_r = (m * point3d.x - h * point3d.z + h * k) / (m + k - point3d.z);
if( abs(x_r) < width/2.0-1){
if(flags[symRound(x_r) + width/2] == 0){
point(symRound(x_r), symRound(y_eye));
flags[symRound(x_r) + width/2] = 1;
color_index[symRound(x_r) + width/2] = loc;
}
x_l = x_r;
} else {
break;
}
}
// 次に初期値を右目からの座標として処理する
x_r = x_ini;
while(true){
// この右目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_r, y_eye, h);
// この対称物体上の点に対応する、左目からの紙上の座標位置を算出する。
x_l = (m * point3d.x + h * point3d.z - h * k) / (m + k - point3d.z);
if( abs(x_l) < width/2.0){
if(flags[symRound(x_l) + width/2] == 0){
point(symRound(x_l), symRound(y_eye));
flags[symRound(x_l) + width/2] = 1;
color_index[symRound(x_l) + width/2] = loc;
}
x_r = x_l;
} else {
break;
}
}
}
}
}
save("stereogram_circleAndRect_inPhoto.jpg");
}
// pixelの大きさを考慮した整数化
int symRound(float p){
if( p < -0.5 ){
return floor(p+0.5);
} else if( p > 0.5 ){
return ceil(p-0.5);
} else {
return 0;
}
}
// 対称物体上の点の位置を算出する関数
PVector get3DPoint(
float x_on_paper, // 紙上の点のx座標
float y_on_paper, // 紙上の点のy座標
float eye_pos_x // 左目の場合-h, 右目の場合h
){
// 視点(左目or右目)と紙上の点を通る直線をパラメータ表示したときの係数
float ax = x_on_paper - eye_pos_x;
float bx = eye_pos_x;
float ay = y_on_paper;
float by = 0.0;
float az = -m;
float bz = m + k;
// 四角形が乗る曲面を2次関数で現したときの係数(z=-A(x+alpha)^2+B)
float A = circle_pos_z / radius / radius;
float B = circle_pos_z * 3.0 / 2.0;
float alpha = 2.0/3.0 * radius;
// 上記の直線と2次関数の曲面との交点を算出するための2次方程式の係数
float a = A * ax * ax;
float b = 2.0 * A * ax *(bx + alpha) + az;
float c = A*(bx + alpha) * (bx + alpha) + bz - B;
// 2次方程式の解
float t = (m+k)/m; // tの初期値(z=0平面と交わる時の値)、解がなければこの値を利用
float tp, zp, tm, zm;
if( abs(a) >= 0.001 && b*b - 4.0*a*c >= 0.0 ){
tp = (-b + sqrt(b*b - 4.0*a*c))/2.0/a;
tm = (-b - sqrt(b*b - 4.0*a*c))/2.0/a;
zp = m + k - m * tp;
zm = m + k - m * tm;
// 2つの解の内、zの値が大きくなるtを選ぶ
if( zp > zm ){
t = tp;
} else {
t = tm;
}
} else if( abs(a) < 0.001 ){
t = -c/b;
}
float x, y, z; // 交点の座標
// 直線と2次関数の曲面との交点、または直線とz=0平面の交点を算出
x = eye_pos_x + (x_on_paper - eye_pos_x)*t;
y = y_on_paper * t;
z = m + k - m * t;
// 真ん中が空いた四角形上に交点が乗っていないか、確認する。
if (z < 0.0 || y > radius/3.0 || y < -radius * 5.0/3.0
|| ( ( x > -3.0/2.0*radius && x < radius/6.0 ) && ( y > -4.0/3.0*radius && y < 0.0 ) )
){
// 乗っていなければ、直線とz=0平面の交点に置き換える
t = (m+k)/m;
x = eye_pos_x + (x_on_paper - eye_pos_x)*t;
y = y_on_paper * t;
z = m + k - m * t;
}
// 次に、直線と円環が乗る平面(z=circle_pos_z)との交点を算出する
float temp_x, temp_y, temp_z;
t = (m+k-circle_pos_z)/m;
temp_x = eye_pos_x + (x_on_paper - eye_pos_x)*t;
temp_y = y_on_paper * t;
temp_z = m + k - m * t;
// 交点が円環上に乗っているかを確認する
if( (sqrt((temp_x-radius/3.0) * (temp_x-radius/3.0) + (temp_y-radius/3.0) * (temp_y-radius/3.0)) <= 4.0/3.0*radius)
&& (sqrt((temp_x-radius/3.0) * (temp_x-radius/3.0) + (temp_y-radius/3.0) * (temp_y-radius/3.0)) >= 2.0/3.0*radius)
&& (temp_z > z) // 円環上の点がz=0平面、または穴の開いた四角形よりz軸方向で上になっているか
){
// 交点を円環上の交点に更新する
x = temp_x;
y = temp_y;
z = temp_z;
}
PVector result = new PVector(x,y,z);
return result;
}