IH8（P2）

ここでは、アイソヘドラルタイリングIH8（P2）について、解説します。

Contents

1 IH8（P2）
- 1.1 IH8（P2）の基本図形のサイズ
- 1.2 IH8（P2）の基本図形を並べる
2 IH8（P2）の基本図形の変形
3 プログラムコード

アイソヘドラルタイリングIH8（P2）の基本図形は以下のような形になります。

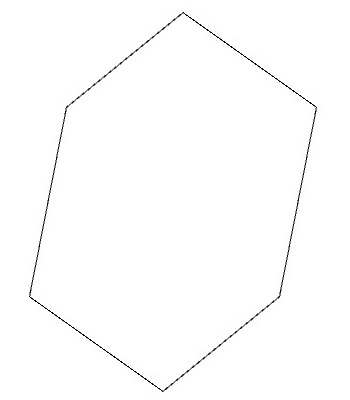
これは、記事「基本図形の形を考える」で示したP2群の基本図形の各辺の長さを調整したものを2つ組み合わせたものになっています。

IH8（P2）の基本図形のサイズ

この基本図形の各辺に以下の図のように、ラベルを振ります。

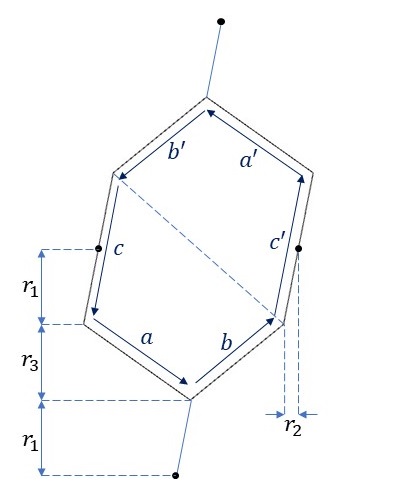
IH8（P2）の基本図形は、上図のように点線で2つの四角形に分けると、各四角形は記事「基本図形の形を考える」で示したP2群の基本図形の各辺の長さを調整したものであり、2つの四角形は同じものになります。つまり、辺\(a\)と辺\(a’\)、辺\(b\)と辺\(b’\)、および辺\(c\)と辺\(c’\)は、それぞれ同じ辺になります。

今回、辺\(c\)の中点、辺\(c’\)の中点が横方向に近接する一般格子点（黒点）となるように設定します。また、縦方向をみると、上図の\(r_1,r_3\)は\(2 r_1+r_3\)が一般格子の縦方向の近接点同士の高さになるように調整します。\(r_2\)は辺\(c\)あるいは辺\(c’\)をどれくらい傾けるかを調整するために利用します。

IH8（P2）の基本図形を並べる

このIH8（P2）の基本図形をP2群の対称性を保ちながら並べると、以下のような図形が得られます。

IH8（P2）の基本図形の変形

基本図形の変形を行うために、基本図形の各辺にラベルをふって、隣り合う基本図形との辺の対応関係を見てみます。

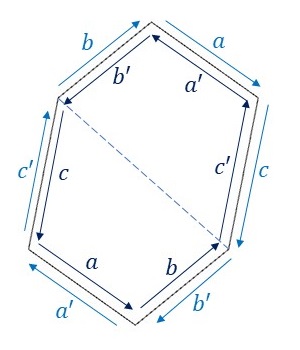
辺\(a\)と辺\(a’\)、辺\(b\)と辺\(b’\)、および辺\(c\)と辺\(c’\)がそれぞれ異なる向きに重なっています。ただ、H8（P2）の基本図形において、点線で分けた2つの四角形は同じものですので、辺\(a\)と辺\(a’\)、辺\(b\)と辺\(b’\)、および辺\(c\)と辺\(c’\)は、それぞれ同じ辺になります。つまり、\(a, b, c\)はそれぞれ両側のラベルが同じで向きが異なると解釈できますので、中点に関して点対称な変形を行います。それにより、隣り合う基本図形同士を重ねることなくP2群の対称性に従って敷き詰めることができます。

ここでは、書籍「装飾パターンの法則」のp.95にあるIH8（P2）の例を参考に、このルールに従ってIH8（P2）の基本図形を下図のように変形してみました。

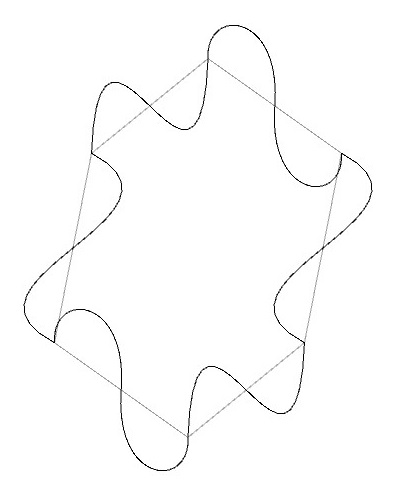
この変形した基本図形をP2群の対称性を考慮して並べていくと、下図のような図形を得ることができます。なお、今回は一般格子点も示しています。

プログラムコード

今回の図形を作成するためのプログラムコードを示します。

PVector[][] lattice; // 格子点ベクトル
PShape tile; // タイル
PVector[] base = new PVector[2]; // 格子を張るベクトル
int col_num = 4; // 描画するタイルの列の数
float scalar; // タイルの辺の長さ

void setup(){
  
  size(1000, 1000, P2D);
  noFill();
  scalar = width * 1.0 / col_num; // 描画ウィンドウと行の数からタイルの大きさを決定
  makeGeneralVector(); // 一般格子を張るベクトルの生成
  makeLattice(); // 格子点ベクトルを生成
  makeTileP2(); // タイルを生成
  drawTiling(); // タイリングを描画
  
  save("IH8_P2_transformation.jpg");
}

// 一般格子を張るベクトルを生成する関数
void makeGeneralVector(){
  base[0] = new PVector(1.0, 0.0);
  base[1] = PVector.fromAngle(PI * 9.5 / 24.0);
  base[1].mult(1.2);
}

// 一般格子を生成する関数
void makeLattice(){
  int row_num = ceil(col_num / base[1].x); // 行の数
  lattice = new PVector[col_num + 3][row_num + 1];
  for (int i = 0; i < col_num + 3; i++){
    for (int j = 0; j < row_num + 1; j++){
      PVector v = PVector.mult(base[0], i * scalar); 
      v.add(PVector.mult(base[1], j * scalar));
      lattice[i][j] = new PVector(v.x % ((col_num+3)*scalar) - 2.0 * scalar, v.y); // x軸方向にscalarの2倍だけ左にシフト
    }
  }
}

// 六角形を変形する関数（基本図形）
PShape transformHexagon(){
  
  PVector[] v = new PVector[6]; // 六角形の頂点
  float r1, r2;
  r1 = 1.0/3.0 * scalar * base[1].y;
  r2 = 2.0/27.0 * scalar * base[0].x;

  v[0] = new PVector(-r2, r1);
  v[1] = new PVector(r2, -r1);
  v[1].add(base[1].copy().mult(scalar));
  v[2] = new PVector(-r2, r1);
  v[2].add(base[0].copy().mult(scalar));
  v[3] = new PVector(r2, -r1);
  v[3].add(base[0].copy().mult(scalar));
  v[4] = new PVector(-r2, r1);
  v[4].add(base[0].copy().mult(scalar));
  v[4].sub(base[1].copy().mult(scalar));
  v[5] = new PVector(r2, -r1);

  // 六角形を変形する
  PShape hexagon = createShape();
  hexagon.beginShape(); 
  PVector[] auxiliary_point = new PVector[5];
  // 辺aを中点で対称に変形する
  hexagon.vertex(v[0].x, v[0].y);
  auxiliary_point[0] = getAuxiliaryPoint(v[0], v[1], -1.0/5.0, -1.0/4.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[0], v[1], 1.0/5.0, -1.0/2.0); 
  auxiliary_point[2] = getAuxiliaryPoint(v[0], v[1], 1.0/2.0, 0.0);
  auxiliary_point[3] = getAuxiliaryPoint(v[0], v[1], 4.0/5.0, 1.0/2.0); 
  auxiliary_point[4] = getAuxiliaryPoint(v[0], v[1], 6.0/5.0, 1.0/4.0); 
  hexagon.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, auxiliary_point[2].x, auxiliary_point[2].y);
  hexagon.bezierVertex(auxiliary_point[3].x, auxiliary_point[3].y, auxiliary_point[4].x, auxiliary_point[4].y, v[1].x, v[1].y);
  // 辺bを中点で対称に変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[1], v[2], 7.0/8.0, -1.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[1], v[2], 1.0/8.0, 1.0); 
  hexagon.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[2].x, v[2].y);
  // 辺c'を中点で対称に変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[2], v[3], 1.0/5.0, -2.0/3.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[2], v[3], 4.0/5.0, 2.0/3.0); 
  hexagon.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[3].x, v[3].y);
  // 辺a'を辺aと同じ形に変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[3], v[4], -1.0/5.0, -1.0/4.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[3], v[4], 1.0/5.0, -1.0/2.0); 
  auxiliary_point[2] = getAuxiliaryPoint(v[3], v[4], 1.0/2.0, 0.0);
  auxiliary_point[3] = getAuxiliaryPoint(v[3], v[4], 4.0/5.0, 1.0/2.0); 
  auxiliary_point[4] = getAuxiliaryPoint(v[3], v[4], 6.0/5.0, 1.0/4.0); 
  hexagon.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, auxiliary_point[2].x, auxiliary_point[2].y);
  hexagon.bezierVertex(auxiliary_point[3].x, auxiliary_point[3].y, auxiliary_point[4].x, auxiliary_point[4].y, v[4].x, v[4].y);
  // 辺b'を辺bと同じ形に変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[4], v[5], 7.0/8.0, -1.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[4], v[5], 1.0/8.0, 1.0); 
  hexagon.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[5].x, v[5].y);
  // 辺cを辺c'と同じ形に変形する
  auxiliary_point[0] = getAuxiliaryPoint(v[5], v[0], 1.0/5.0, -2.0/3.0); 
  auxiliary_point[1] = getAuxiliaryPoint(v[5], v[0], 4.0/5.0, 2.0/3.0); 
  hexagon.bezierVertex(auxiliary_point[0].x, auxiliary_point[0].y, auxiliary_point[1].x, auxiliary_point[1].y, v[0].x, v[0].y);

  hexagon.endShape();
  
  return hexagon;
}

// 辺を変形するために必要な補助点を算出する関数
PVector getAuxiliaryPoint(
  PVector start,
  PVector end, 
  float parallel_size,
  float vertical_size
){
  PVector dir_parallel = end.copy().sub(start.copy());
  PVector dir_vertical = new PVector(-dir_parallel.y, dir_parallel.x);
  PVector auxiliary_point = start.copy().add(dir_parallel.copy().mult(parallel_size)).add(dir_vertical.copy().mult(vertical_size));
  return auxiliary_point;
}

// タイルを生成する関数
void makeTileP2(){
  tile = createShape(GROUP); // PShapeのグループを作る 
  PShape hexagon = transformHexagon(); // 変形した六角形の生成
  tile.addChild(hexagon); // グループに追加
}

// 格子形状に合わせたタイリングを描画する関数
void drawTiling(){
//  background(255);
  for (int i=0; i<lattice.length; i++){
    for (int j=0; j<lattice[0].length; j++){
      tile.resetMatrix();
      tile.translate(lattice[i][j].x, lattice[i][j].y); // タイルの位置を指定
      shape(tile); // タイルを描画
    }
  }
  
  // 格子点を描く
  for (int i=0; i<lattice.length; i++){
    for (int j=0; j<lattice[0].length; j++){
      circle(lattice[i][j].x, lattice[i][j].y, 10);
    }
  }
}