アイソヘドラルタイリングについて引き続き勉強中です。
書籍「装飾パターンの法則」のp.94-107にまとめてある、全部で93種類のアイソヘドラルタイリングと、記事「基本図形の形を考える」で紹介していた各壁紙群の基本図形と照らし合わせて、自分の理解を整理しています。
93種類全てを照らし合わせましたが、いくつかは記事「基本図形の形を考える」で紹介していた基本図形では説明できないものがありました。
具体的には、IH2(pg)、IH5(pgg)、IH25(pgg)、IH39(p6)、IH59(pgg)の5つ。
昨日(8月26日)までに、IH2(pg)、IH5(pgg)の2つについては新たな基本図形であることがわかり、IH25(pgg)はIH5(pgg)の基本図形の1辺を一点に縮めることで再現できることがわかりました。
前置きが長くなりましたが、本日(8月27日)はIH39(p6)、IH59(pgg)の2つについて調査しています。
順番は前後しますが、まずIH59(pgg)について確認。これは昨日から考えていたのですが、なかなか思いつかず、時間がかかってしまいました。でも、気づいてしまうと簡単でした。IH86(pgg)を2つ組み合わせたものでした。詳細については今後説明したいと思います。
次に、IH39(p6)を確認。こちらも時間がかかりましたが、なんとか理解できました。
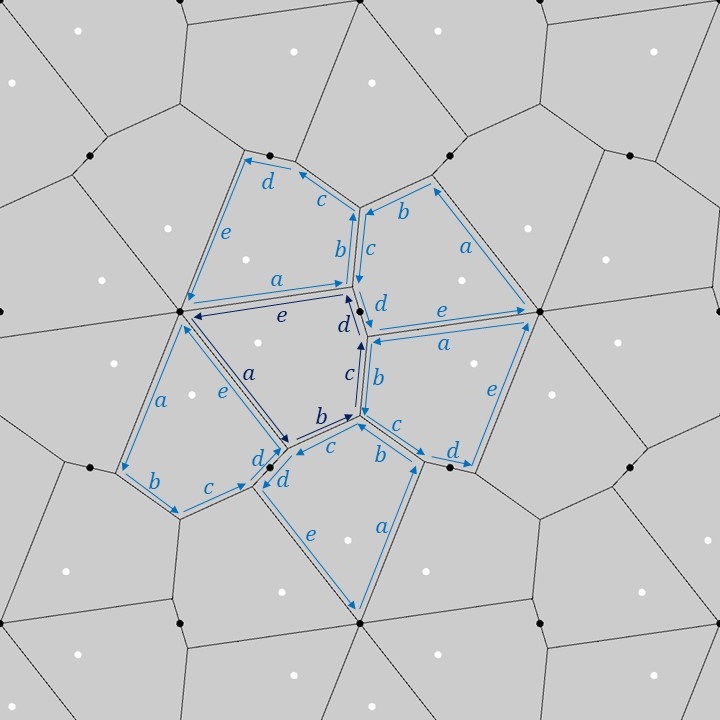
P6群の基本図形の辺\(a,e\)を一点に縮めていくと、辺\(d\)が伸びていってその端点が三角格子の頂点と一致し、また、辺\(b\)と辺\(c\)の共有しない端点についてもそれぞれ三角格子の頂点の位置に移動します。その結果、IH39(p6)を再現することができます。
以上より、アイソヘドラルタイリング93種類全てを再現するめどがたちました。
今後は、これらの内容をサイトにまとめていきたいと思います。