壁紙アートというと、壁に描かれた絵というイメージがあると思います。まあそうなのですが、ここで扱う「壁紙」はある方向に一定距離だけ全体的にずらしたり、ある特定の点の周りで一定の角度だけ回したり、ある特定の軸で反転させたりしてもその模様が変わらないような図形、つまり何らかの対称性をもった図形を扱います。例えば、次のような模様の図形になります。



上の3つの図形を眺めるとわかるとなんとなく想像がつくと思いますが、このような図形の描き方として1つの基本となる図形を描き、それを回転させたり、反転させたりしながら敷き詰めていくことで実現できそうだということがわかります。
壁紙の対称性は17パターン
上の3つの図形のように1つの基本となる図形を決めてそれをきちんと隙間なく敷き詰めていく方法は、図形の対称性の観点からみると、17パターンしかありません。ここでは、これら17パターンを紹介していきたいと思います。
※ここで紹介する対称性の17パターンは壁紙群(または文様群)で分類することができます。壁紙群に関しては、学習院大学の川﨑徹郎先生のサイト「文様の幾何学」が非常にわかりやすいです。また、以下の解説において利用している用語はこの川崎先生のサイトを参考にしています。
対称性を考えるための準備
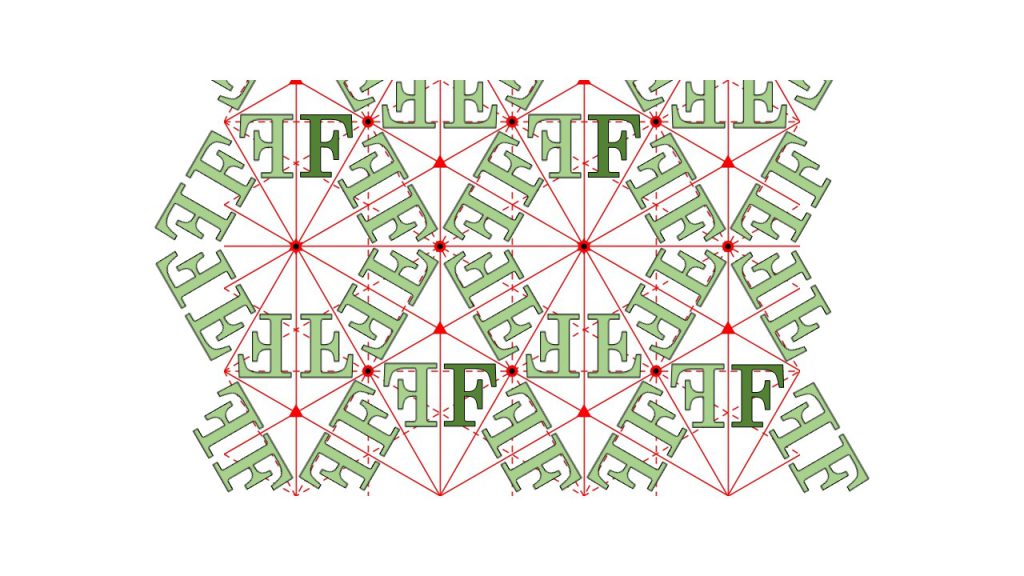
このような図形の対称性を考える際には、図形を抽象化して図形の特徴を表す「格子」と「基本となる二つの方向」を考えると分類しやすくなります。例えば、例に挙げている3つの図に「格子」と「二つの方向」の矢印を書き入れてみると下図の黒点と赤矢印のようになります。



左の図形をみると、すべての黒点を赤矢印の方向にずらしたり、適当な黒点を選びその周りで180°回転させたりしてもその図形の模様は変わらないことがわかります。また、真ん中の図形をみると、すべての黒点を赤矢印の方向に2つ分ずらしたり、適当な黒点の周りで90°または180°回転させたりしてもその図形の模様は変わらないことがわかります。最後に右の図形をみると、 すべての黒点を赤矢印の方向に2つ分ずらしたり、適当な黒点の周りで60°回転させたりしてもその図形の模様は変わらないことがわかります。 これらの考察で重要なことは、これらの操作を行っても格子(黒点)の位置は変わっていないことです。
実は、壁紙の対称性はまずここで描いたような格子に対する対称性を考え、次にその対称性から描かれた模様も考慮して取捨選択していくことで17パターンに分類することができます。つまり、格子模様に対してずらしたり、回転させたりしてもその格子の位置が変わらないようなものを考えていくことが、対称性の分類を考える第一歩になります。
5種類の格子形状と対称性
格子の取り方は 一般格子、長方格子、正方格子、菱形格子、三角格子の 5種類があります。「壁紙」の対称性である17パターンはこれら5種類の格子形状を並進移動、回転、鏡映、滑り鏡映(並進移動+鏡映)に対して不変になるような図形を考えていくことで分類することができます。
以下では、格子形状とそれらの格子に対して考えられる対称性を考えて分類していきます。
一般格子での対称性はP1,P2の2パターン
一般格子は次のような格子形状をしています。特徴としては近傍の4点を考えると、平行四辺形を形作ることが分かります。

このような一般格子が不変になるような対称性を考えてみると、並進移動の他、下の図のような赤点周りの180°回転が考えられます。

では、この一般格子の対称性を持つような図形を考えてみます。
P1群
まず、次のような図形が考えられます。

このような図形はP1群と呼ばれているもので、一般格子の対称性のうち、並進移動のみを持っています。
P2群
次は、P2群と呼ばれている対称性をもつ図形になります。この図形は一般格子の対称性をすべて持ったものとなります。

長方格子での対称性はPM,PG,PMM,PMG,PGGの5パターン
長方格子は次のような格子形状をしています。特徴としては近傍の4点を考えると、長方形を形作ることが分かります。

このような長方格子が不変になるような対称性を考えてみると、並進移動の他、下の図のような赤点周りの180°回転、赤線を軸とする鏡映変換が考えられます。
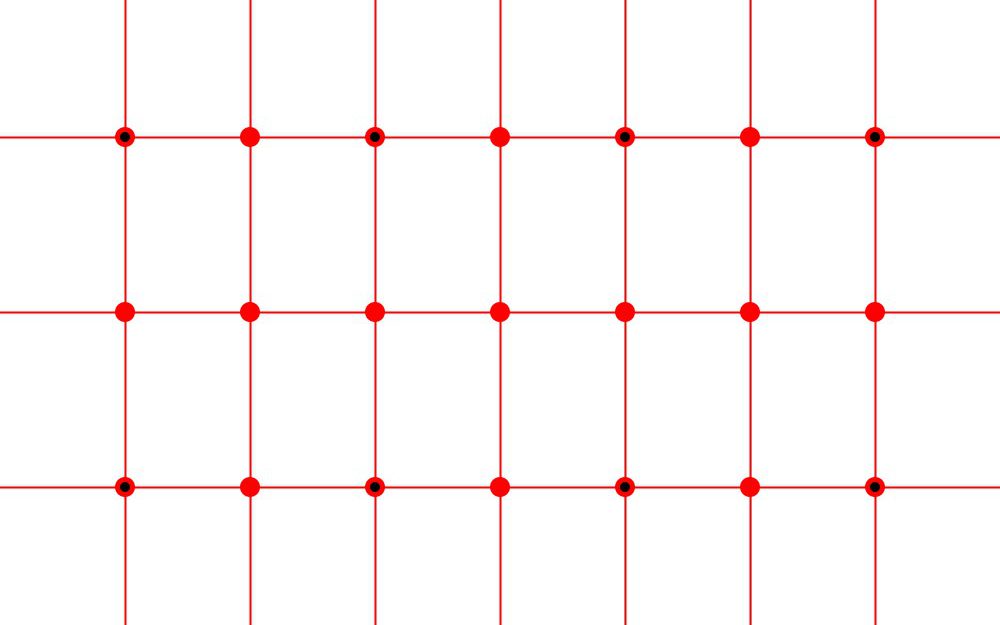
では、この長方格子の対称性を持つような図形を考えてみます。
PM群
まず、PM群と呼ばれている対称性をもつ図形になります。この図形は長方格子の一方向のみの鏡映対称性のみを持ったものとなります。
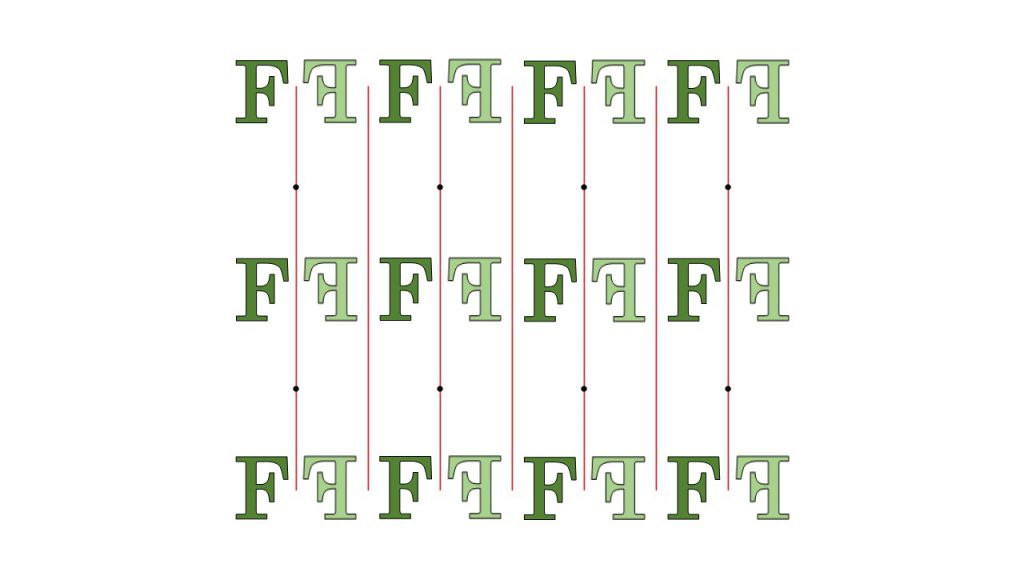
PG群
次は、PG群と呼ばれている対称性をもつ図形になります。この図形は長方格子の一方向のみに滑り鏡映(並進移動と鏡映を合わせたもの)対称性を持ったものとなります。
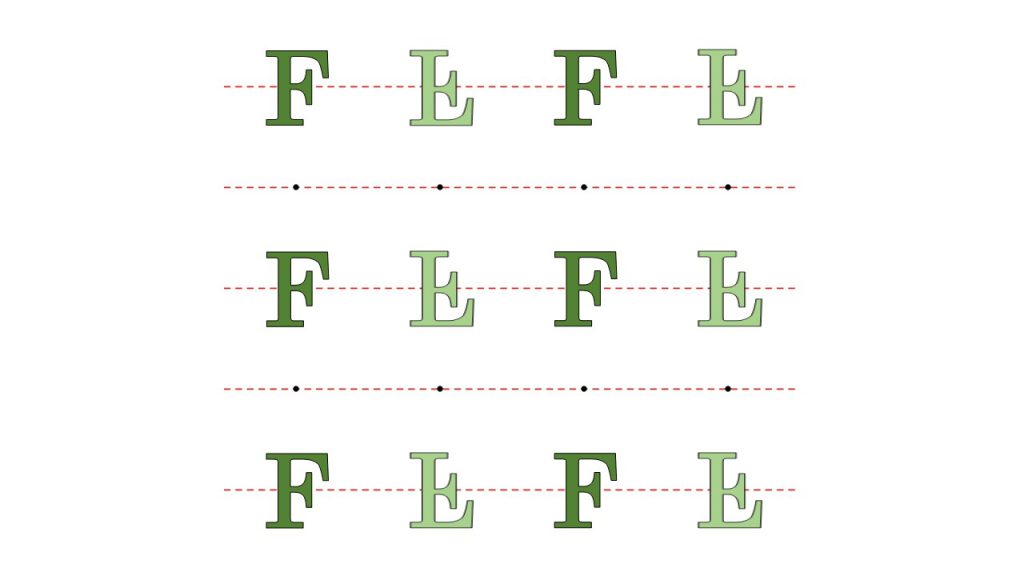
PMM群
次は、PMM群と呼ばれている対称性をもつ図形になります。この図形は長方格子の対称性をすべて持ったものとなります。
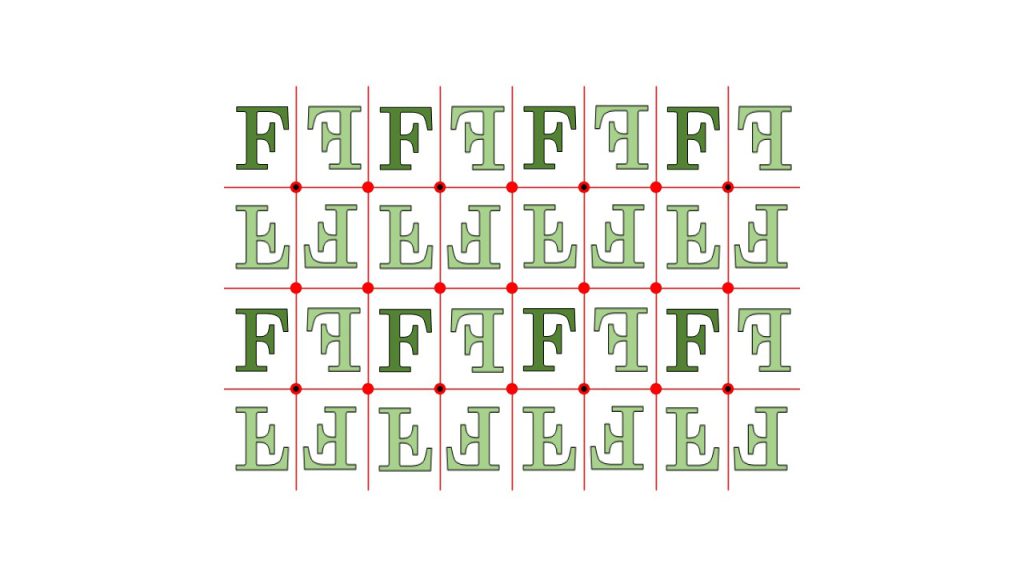
PMG群
次は、PMG群と呼ばれている対称性をもつ図形になります。この図形は長方格子の対称性のうち、下図のように180°回転、鏡映、滑り鏡映を持ったものとなります。
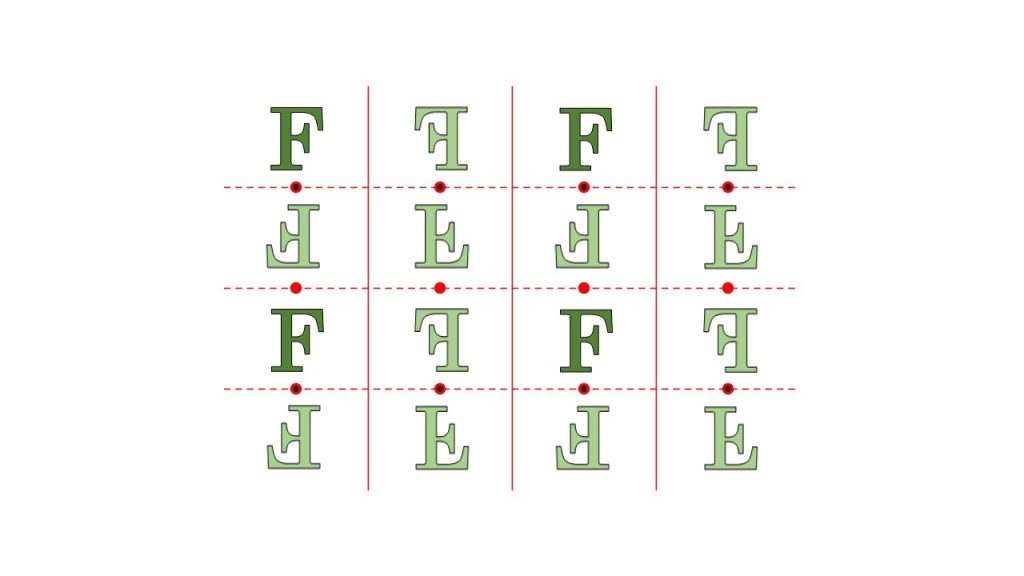
PGG群
次は、PGG群と呼ばれている対称性をもつ図形になります。この図形は長方格子の対称性のうち、下図のように180°回転、滑り鏡映を持ったものとなります。
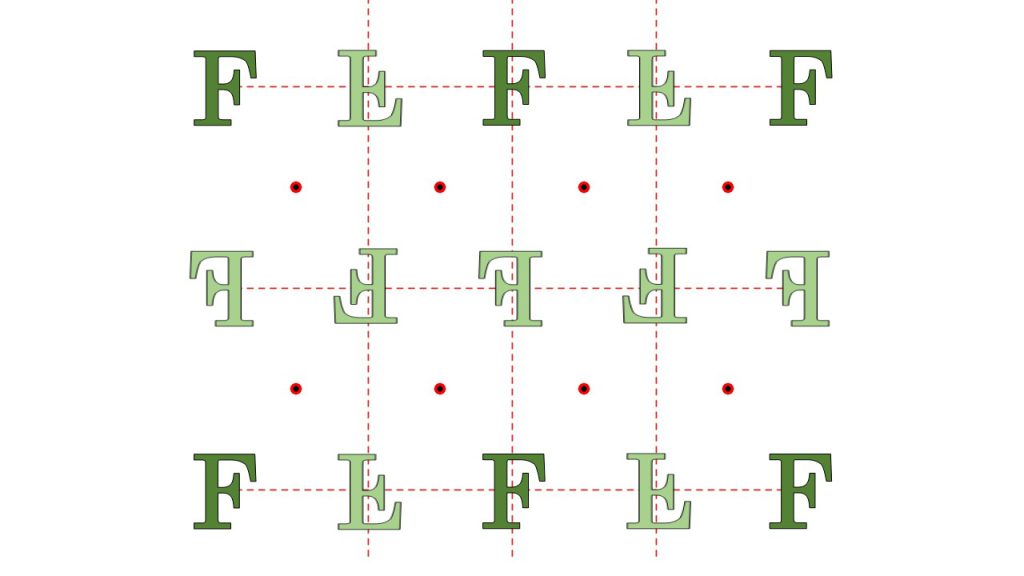
菱形格子での対称性はCM,CMMの2パターン
菱形格子は次のような格子形状をしています。特徴としては近傍の4点を考えると、菱形を形作ることが分かります。

このような菱形格子が不変になるような対称性を考えてみると、並進移動の他、下の図のような赤点周りの180°回転、赤線を軸とする鏡映変換が考えられます。
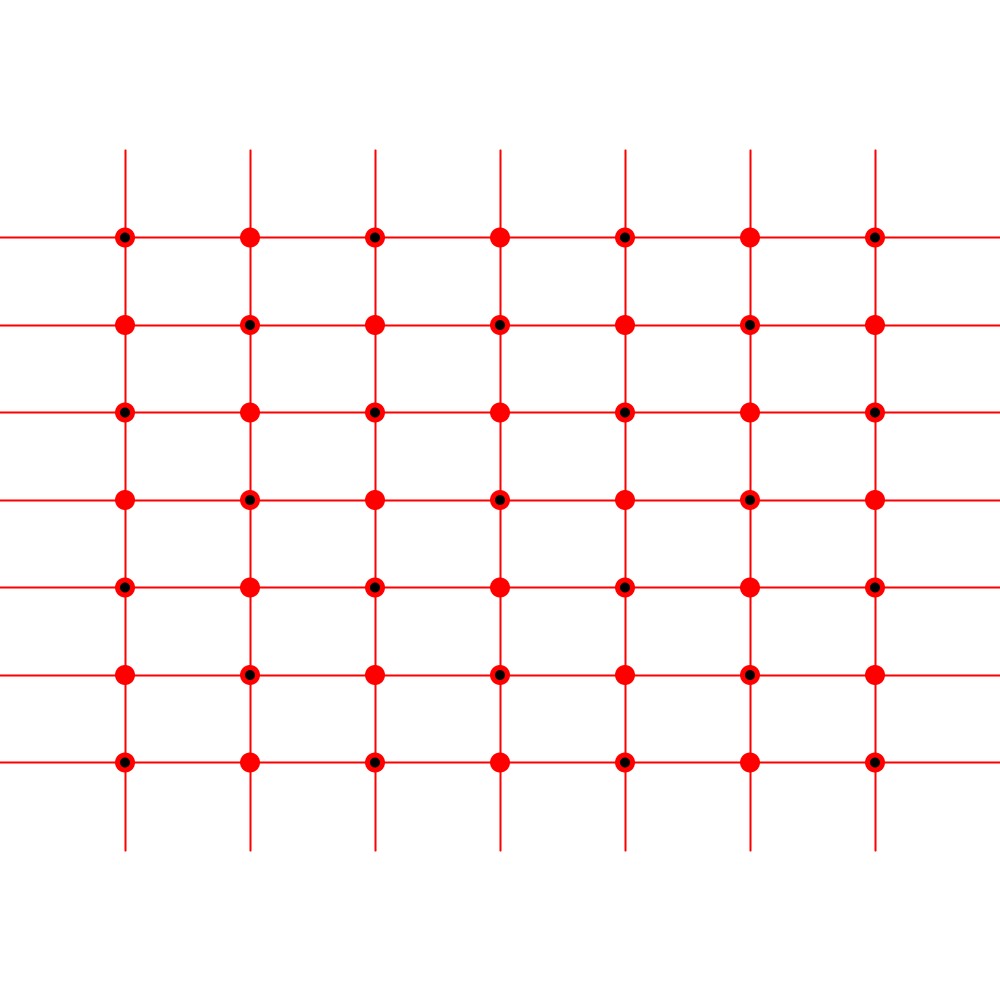
では、この菱形格子の対称性を持つような図形を考えてみます。
CM群
まず1つ目は、CM群と呼ばれている対称性をもつ図形になります。この図形は格子の一方向に対して鏡映と滑り鏡映対称性を交互に持ったものとなります。
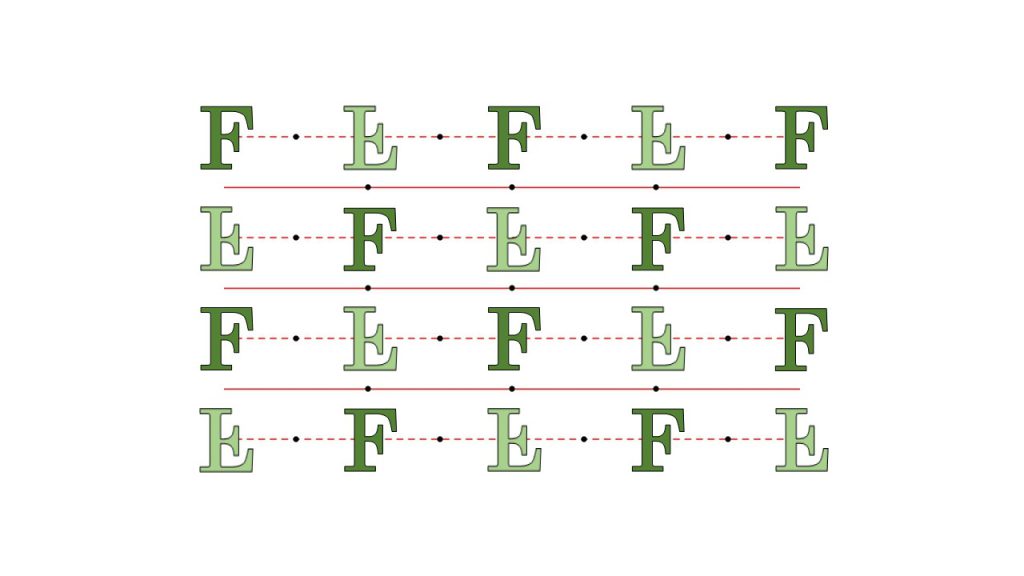
CMM群
2つ目は、CMM群と呼ばれている対称性をもつ図形になります。この図形は下の図のような赤点周りの180°回転、 及び格子の2つの直交する方向に対してそれぞれ鏡映と滑り鏡映対称性を交互に持ったものとなります。

正方格子での対称性はP4,P4M,P4Gの3パターン
正方格子は次のような格子形状をしています。特徴としては近傍の4点を考えると、正方形を形作ることが分かります。

このような正方格子が不変になるような対称性を考えてみると、並進移動の他、下の図のような赤丸点周りの180°回転、赤四角点周りの90°回転、および赤線を軸とする鏡映変換が考えられます。

では、この正方格子の対称性を持つような図形を考えてみます。
P4群
まず1つ目は、P4群と呼ばれている対称性をもつ図形になります。この図形は下図のように赤丸点周りの180°回転、赤四角点周りの90°回転の対称性を持ったものとなります。

P4M群
2つ目は、P4M群と呼ばれている対称性をもつ図形になります。この図形は下図のように赤丸点周りの180°回転、赤四角点周りの90°回転、縦横方向に鏡映、斜め方向に鏡映と滑り鏡映対称性を交互に持ったものとなります。

P4G群
3つ目は、P4G群と呼ばれている対称性をもつ図形になります。この図形は下図のように赤丸点周りの180°回転、赤四角点周りの90°回転、縦横方向に滑り鏡映、斜め方向に鏡映と滑り鏡映対称性を交互に持ったものとなります。

三角格子での対称性はP3,P3M1,P31M,P6,P6Mの5パターン
三角格子は次のような格子形状をしています。特徴としては近傍の3点を考えると、正三角形を形作ることが分かります。

このような三角格子が不変になるような対称性を考えてみると、並進移動の他、下の図のような赤三角点周りの120°回転、赤六角星形点周りの60°回転、赤線を軸とする鏡映変換、および赤点線を軸とする滑り鏡映が考えられます。

では、この三角格子の対称性を持つような図形を考えてみます。
P3群
まず1つ目は、P3群と呼ばれている対称性をもつ図形になります。この図形は下図のように赤三角点周りの120°回転の対称性を持ったものとなります。
P3M1群
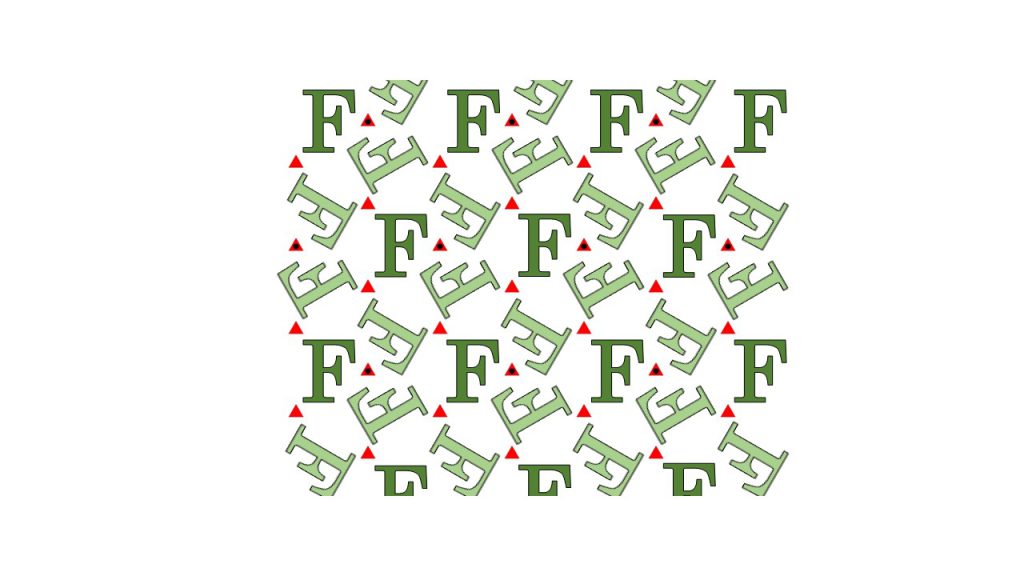
2つ目は、P3M1群と呼ばれている対称性をもつ図形になります。この図形は下図のように赤三角点周りの120°回転、赤線を軸とする鏡映、赤点線を軸とする滑り鏡映の対称性を持ったものとなります。
P31M群
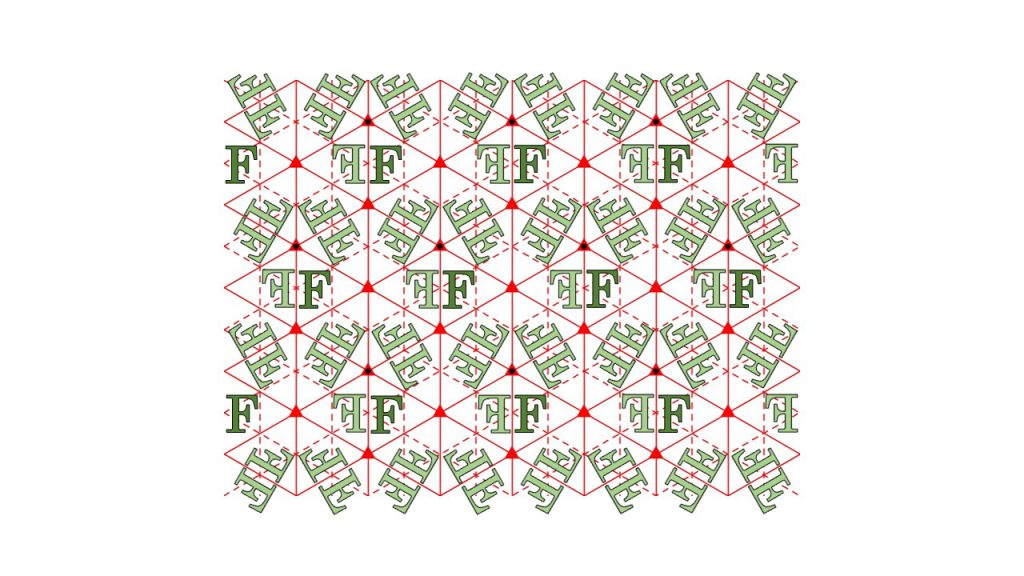
3つ目は、P31M群と呼ばれている対称性をもつ図形になります。この図形は下図のように赤三角点周りの120°回転、赤線を軸とする鏡映、赤点線を軸とする滑り鏡映の対称性を持ったものとなります。
P6群
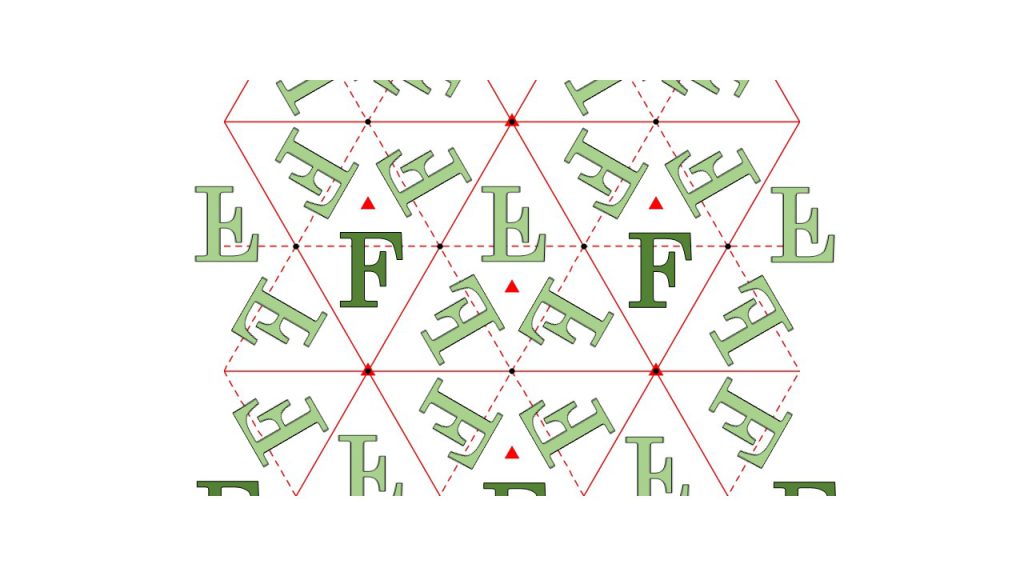
4つ目は、P6群と呼ばれている対称性をもつ図形になります。この図形は下図のように赤丸点周りの180°、赤三角点周りの120°回転、赤六角星形点周りの60°回転の対称性を持ったものとなります。
P6M群
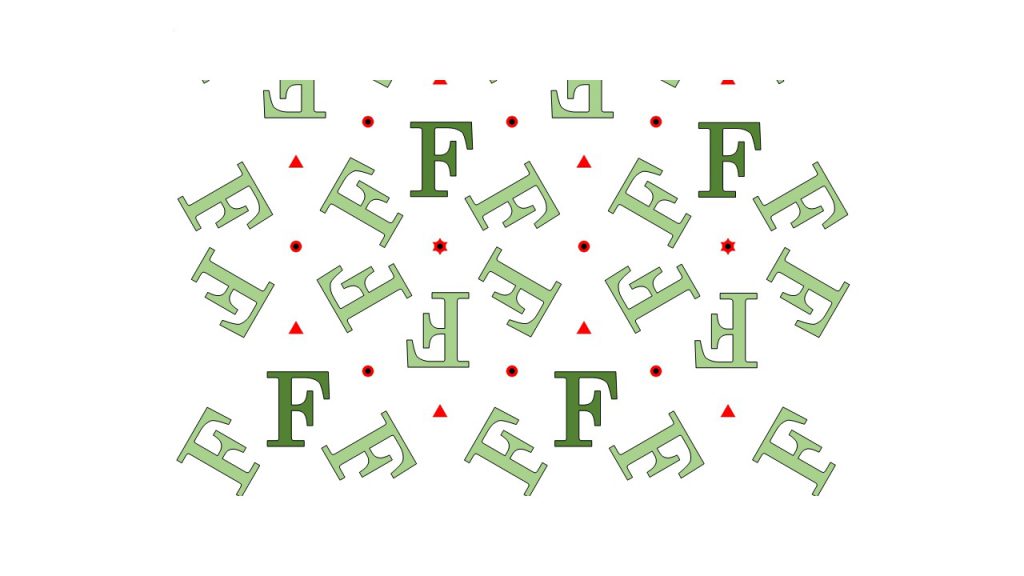
5つ目は、P6M群と呼ばれている対称性をもつ図形になります。この図形は下図のように 赤丸点周りの180° 赤三角点周りの120°回転、赤六角星形点周りの60°回転、赤線を軸とする鏡映、赤点線を軸とする滑り鏡映 の対称性を持ったものとなります。
壁紙アートの描き方
基本図形
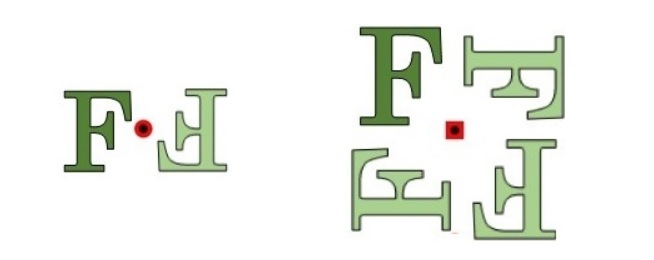
壁紙アートはある図形を回転させたり、反転させたりしながら並べていくことで作ることができます。このとき、最小単位となる図形を基本図形と呼ぶことにします。上記で17パターンの例を図で紹介してきましたが、そのときの「F」の部分が基本図形となります。
タイル
壁紙アートは基本図形を回転させたり、反転させたりして順に並べていくことで作成できますが、基本図形をそのまま扱うよりも基本図形をいくつか集めたものを準備して、これを並べていく方がより効率的に作成することができます。この集めたものをタイルと呼んでいます。
壁紙アート作成の流れ
したがって、壁紙アート作成の流れは以下のようになっています。
- 格子形状を準備する
- 基本図形を作成する
- 基本図形を組み合わせてタイルを作成する
- タイルを格子形状に合わせて並べていく
今後、壁紙アートを作成していく際には基本的にこの流れで作成していきます。
なお、壁紙アートの作成については書籍「数学から創るジェネラティブアート」を参考にしています。プログラムコードなども載っており、非常にわかりやすいので、より詳しくはこちらの書籍をご覧ください。