ここでは、書籍「M.C.エッシャーと楽しむ算数・数学パズル」のp.34-35に紹介されている「イスラムタイル」を鳥の形に変形したものをProcessingで再現してみました。なお、描き方は別記事「イスラムタイル」で紹介したものとほぼ同じですので、ポイントだけ解説したいと思います。
鳥の形
今回描いてみたイスラムタイルを鳥の形に変形したものは以下のような図形になりました。

描き方
この図形の描き方は別記事「イスラムタイル」で紹介したものとほぼ同じで、違いはP4G群の基本図形の辺\(b\)と辺\(c\)の変形の仕方になります。
P4G群の基本図形の変形
P4G群の図形で隣り合う基本図形同士の辺のラベルと向きは以下のようになります。
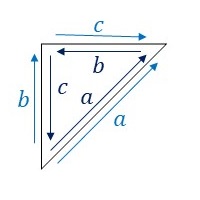
今回の鳥の形にするため、辺\(b\)を以下の図のように変形します。
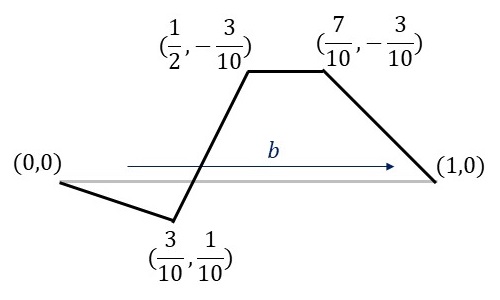
辺\(c\)の変形は辺\(b\)で変形したものを辺\(c\)の部分に反対向きに置くことで実現できます。これらを実施した結果、P4G群の基本図形は鳥の形(の半分)の基本図形に変形することができます。
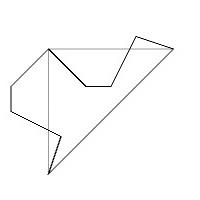
プログラムコード
最後に、プログラムコードを載せておきます。基本は別記事「イスラムタイル」に記載しているプログラムコードと同じで、transformIsoscelesRightTriangle関数のみ書き換えればよいので、その部分のみを示します。
// 直角二等辺三角形を変形する関数(基本図形)
PShape transformIsoscelesRightTriangle(){
PVector[] v = new PVector[3]; // 直角二等辺三角形の頂点
PShape isosceles_right_triangle = createShape();
v[0] = base[0].copy().mult(-scalar / 2.0).add(base[1].copy().mult(scalar));
v[1] = base[0].copy();
v[1].mult(scalar / 2.0);
v[2] = base[0].copy();
v[2].mult(-scalar / 2.0);
// 直角二等辺三角形を変形する
isosceles_right_triangle.beginShape();
PVector[] auxiliary_point = new PVector[3];
// 辺aは変形できず、直線のみ。
isosceles_right_triangle.vertex(v[0].x, v[0].y);
isosceles_right_triangle.vertex(v[1].x, v[1].y);
// 辺bをベジエ曲線で変形する
auxiliary_point[0] = getAuxiliaryPoint(v[1], v[2], 3.0/10.0, 1.0/10.0);
auxiliary_point[1] = getAuxiliaryPoint(v[1], v[2], 1.0/2.0, -3.0/10.0);
auxiliary_point[2] = getAuxiliaryPoint(v[1], v[2], 7.0/10.0, -3.0/10.0);
isosceles_right_triangle.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
isosceles_right_triangle.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
isosceles_right_triangle.vertex(auxiliary_point[2].x, auxiliary_point[2].y);
isosceles_right_triangle.vertex(v[2].x, v[2].y);
// 辺cを辺bと同じ形で逆向きに変形する
auxiliary_point[0] = getAuxiliaryPoint(v[0], v[2], 3.0/10.0, 1.0/10.0);
auxiliary_point[1] = getAuxiliaryPoint(v[0], v[2], 1.0/2.0, -3.0/10.0);
auxiliary_point[2] = getAuxiliaryPoint(v[0], v[2], 7.0/10.0, -3.0/10.0);
isosceles_right_triangle.vertex(auxiliary_point[2].x, auxiliary_point[2].y);
isosceles_right_triangle.vertex(auxiliary_point[1].x, auxiliary_point[1].y);
isosceles_right_triangle.vertex(auxiliary_point[0].x, auxiliary_point[0].y);
isosceles_right_triangle.endShape(CLOSE);
return isosceles_right_triangle;
}