ここでは、ランダムドット・ステレオグラムを紹介したいと思います。ランダムドット・ステレオグラムは、一見適当にプロットされた点の集まりのように見える図形の中に、立体視することでなんらかの図形が立体的に浮かび上がってくるというものです。なお、ここでの解説は書籍「ステレオグラムをつくろう―あなたも3Dアーティスト」のp.52-61を参考にしています。
Contents
ランダムドット・ステレオグラムの原理
立体視の原理(復習)
記事「正四面体を立体視する」で立体視の原理について説明しました。
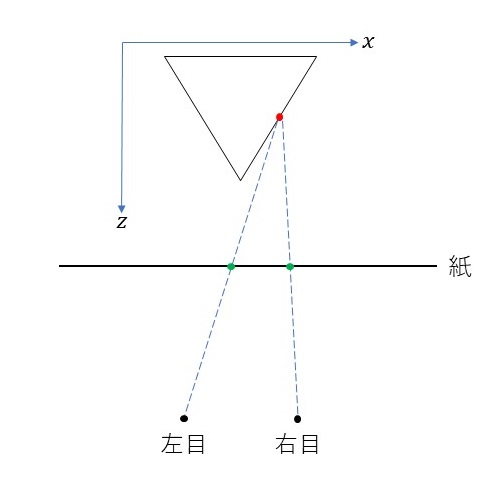
おさらいしておくと、正四面体上のある一点(赤点)をz軸方向から見ることを考えます。そのときの両目の位置を上図のように配置します(黒点)。両目から赤点をみるときの視線は点線のようになります。ここで、両目と正四面体の間に紙をはさみます。このとき、赤点をみるときの視線と紙が交わる点は緑色の点のようになります。これら左目用の緑色の点と右目用の緑色の点を紙上にプロットします。これを立体視したい立体図形上の点、たとえば立体図形の辺上の点について紙上にプロットしていけば、立体視できる図形を作成することができます。
紙上にプロットする点の位置の計算手順
今回のランダムドット・ステレオグラムでも同じ原理で作成することができます。ただし、一つ注意する必要があります。それは立体図形の部分だけでなく、背景も含めた紙上にプロットされる部分全体についても考慮しなくてはならないことです。
- どんな立体を見るのかを決め、関数または他の方法でその立体のデータ(情報)を与える。
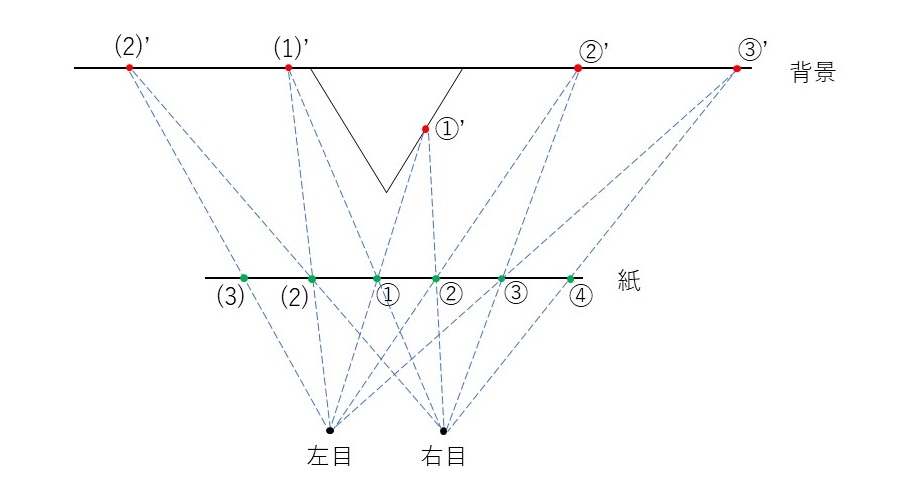
- 紙上の範囲にひとつの点をランダムに描き、①として左目用の点とする。
- 左目の位置と①の点の延長線上に立体との交点①’を求め、①’を右目で見たときの紙上の点②を求め、点を描く。
- 点②を左目用の点とみなし、3を実行する。この処理を点が紙上から外れるまで繰り返し行う。
- 今度は2の①を右目用として、右目の位置と①の点の延長線上に立体との交点(1)’を求め、(1)’を左目で見たときの紙上の点(2)を求め、点を描く。
- 点(2)を右目用の点とみなし、5を実行する。この処理を点が紙上から外れるまで繰り返し行う。
- 2から6までの処理を好きなだけ繰り返す。
なぜこういう手順を行うのか
記事「正四面体を立体視する」でも立体視のやり方のところで、『この画像を紙に印刷して、紙と目を近づけていってください。そうすると、紙上の2つの正四面体が3つの正四面体に見えるようになってきます。』と書きました。この3つの正四面体がなぜ見えるのか。これを考えると分かってきます。
画像上には「左目用の正四面体」と「右目用の正四面体」が描かれますが、「左目用の正四面体」を左目だけで見て「右目用の正四面体」を右目だけで見る、というわけにはいきません。実際には「左目用の正四面体」を左目だけでなく右目でも見ていて、「右目用の正四面体」を右目だけでなく左目でも見ているわけです。それが「3つの正四面体が見える」ことにつながります。つまり、3つの正四面体は
- 左の正四面体 → 「左目用の正四面体」を右目で見たときの像
- 中央の正四面体 → 「左目用の正四面体」を左目、「右目用の正四面体」を右目で見たときの像
- 右の正四面体 → 「右目用の正四面体」を左目で見たときの像
となります。
記事「正四面体を立体視する」で描いた図形では、中央の像のみに注目して、左右の像は無視していましたが、ランダムドット・ステレオグラムでは紙全体を見ることになるので、左目用の点が右目で見たときにどのように見えるのか、あるいはその逆のことを考慮しておく必要があるということです。
正四面体でのランダムドット・ステレオグラム
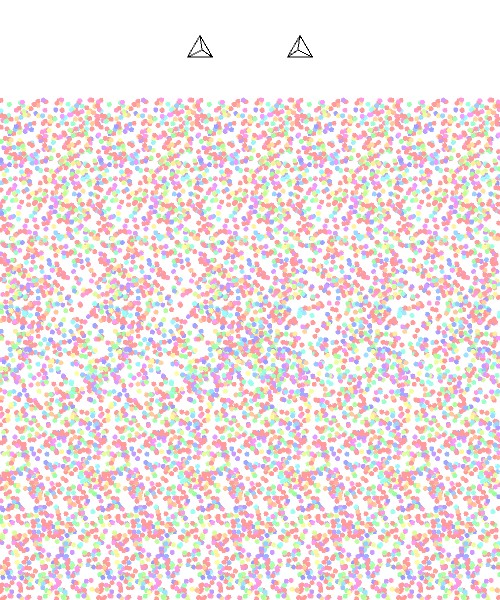
例として、正四面体でのランダムドット・ステレオグラムを作成してみます。結果は以下の通りです。
視線と立体との交点の算出
ランダムドット・ステレオグラムを作成する際に一番苦労するところは目の位置と紙上の点の位置との延長線上に立体との交点を求めるところです。これができれば、後の処理は比較的簡単に処理できます。
正四面体の場合は、次のように行いました。
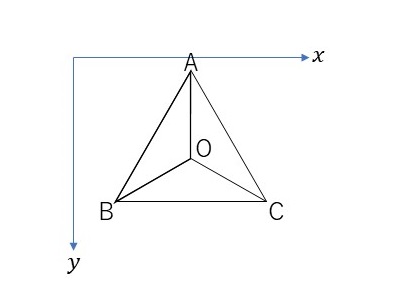
- △OBCを含む平面の方程式を求める。
- 目の位置と紙上の点の位置とを結ぶ直線の方程式を求める。
- 1と2の方程式から交点を求める。
- この交点が△OBCの内部に入っているかを判定する。入っていれば、これを立体との交点として利用する。入っていなければ、背景の平面(\(z=0\)と2で求めた方程式の交点に置き換えて利用する。
- △OAB、△OCAについても1から4までの手順を行う。
- △OBC、△OAB、△OCAの交点が2つ以上見つかった場合、\(z\)座標が大きい方の交点を採用する。
ランダムドット・ステレオグラムの見方
正四面体のランダムドット・ステレオグラムを紙に印刷してください。そして、その紙を少しずつ自分の目に近づけていってください。そうすると、上部の2つの図形が3つに見えるようになってきます。そのあたりで紙の位置を前後に微調整しながら、さらに根気強くピントを合わせていくと、3つに見える図形のうち、真ん中の図形が正四面体の形で飛び出て見えるようになります。このとき、下の点の集まりの中にぼんやりと何かが浮かび上がってきます。うまく下の図形に視線を移すことができれば、その浮かび上がってきた図形が何かわかるはずです。
プログラムコード
正四面体のランダムドット・ステレオグラムを作成したときのプログラムコード(Processing)を載せておきます。
float k = 500.0; // 座標原点から紙までの距離
float m = 500.0; // 紙から目までの距離
float h = 100.0; // 目と目の間の距離の半分
float s = 400.0; // ランダムドット・ステレオグラムで作る正四面体の一辺の長さ
void setup(){
size(500,600,P2D);
background(255,255,255);
PVector point3d; // 立体視したい図形上の点
float x_r, x_l, y_eye; // 紙上の点
float triangular_pyramid_size = 50.0; // 三角錐のサイズ
// 三角錐の4つの頂点のベクトル
PVector triangular_pyramid[] = new PVector[4];
triangular_pyramid[0] = new PVector(0.0, 0.0, sqrt(2.0/3.0)*triangular_pyramid_size);
triangular_pyramid[1] = new PVector(0.0, -1.0/sqrt(3.0)*triangular_pyramid_size, 0.0);
triangular_pyramid[2] = triangular_pyramid[1].copy().rotate(radians(120));
triangular_pyramid[3] = triangular_pyramid[1].copy().rotate(radians(240));
translate(width/2, 50);
// 紙の上に三角錐を左目用と右目用にそれぞれ射影する
for(int i=0; i<4; i++){
for(int j=i+1; j<4; j++){
for(int d=0; d<100; d++){
point3d = triangular_pyramid[i].copy().add(triangular_pyramid[j].copy().sub(triangular_pyramid[i].copy()).mult(d/100.0));
x_r = (m * point3d.x - h * point3d.z + h*k) / (m + k - point3d.z);
x_l = (m * point3d.x + h * point3d.z - h*k) / (m + k - point3d.z);
y_eye = m * point3d.y / (m + k - point3d.z);
point(x_r, y_eye);
point(x_l, y_eye);
}
}
}
translate(0, 300);
float x_ini, y_ini;
for(int i=0; i<2000; i++){
colorMode(HSB);
fill(random(360),100,1000);
noStroke();
x_ini = random(width)-width/2; // 紙上の点の初期値x座標
y_ini = random(width)-width/2; // 紙上の点の初期値y座標
// まず初期値が左目からの座標として処理する
x_l = x_ini;
y_eye = y_ini;
ellipse(x_l, y_eye, 5, 5);
while(true){
// この左目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_l, y_eye, -h);
// この対称物体上の点に対応する、右目からの紙上の座標位置を算出する。
x_r = (m * point3d.x - h * point3d.z + h * k) / (m + k - point3d.z);
if( abs(x_r) < width/2.0 ){
ellipse(x_r, y_eye, 5, 5);
x_l = x_r;
} else {
break;
}
}
// 次に初期値を右目からの座標として処理する
x_r = x_ini;
while(true){
// この右目からの位置に対応する対称物体の上の点の位置を算出する。
point3d = get3DPoint(x_r, y_eye, h);
// この対称物体上の点に対応する、左目からの紙上の座標位置を算出する。
x_l = (m * point3d.x + h * point3d.z - h * k) / (m + k - point3d.z);
if( abs(x_l) < width/2.0 ){
ellipse(x_l, y_eye, 5, 5);
x_r = x_l;
} else {
break;
}
}
}
save("stereogram_triangular_pyramid_randomdot.jpg");
}
// 対称物体上の点の位置を算出する関数
PVector get3DPoint(
float x_on_paper, // 紙上の点のx座標
float y_on_paper, // 紙上の点のy座標
float eye_pos_x // 左目の場合-h, 右目の場合h
){
// 視点(左目or右目)と紙上の点を通る直線をパラメータ表示したときの係数
float ax = x_on_paper - eye_pos_x;
float bx = eye_pos_x;
float ay = y_on_paper;
float by = 0.0;
float az = -m;
float bz = m + k;
float t1, t2, t3;
float x, y, z;
// 視線と正四面体の交点が△OBCに含まれるか
t1 = (k+m-sqrt(2.0/3.0)*s)/(-2.0*sqrt(2.0) * y_on_paper + m);
x = ax * t1 + bx;
y = ay * t1 + by;
z = az * t1 + bz;
if( z < 0.0
|| x/sqrt(3.0)+y < 0.0
|| -x/sqrt(3.0)+y < 0.0
){
t1 = (m+k)/m;
}
// 視線と正四面体の交点が△OABに含まれるか
t2 = ((k+m-sqrt(2.0/3.0)*s)/sqrt(2.0) - sqrt(3.0)*eye_pos_x)/(sqrt(3.0)*(x_on_paper - eye_pos_x) + y_on_paper + m / sqrt(2.0));
x = ax * t2 + bx;
y = ay * t2 + by;
z = az * t2 + bz;
if( z < 0.0
|| x > 0.0
|| x/sqrt(3.0)+y > 0.0
){
t2 = (m+k)/m;
}
// 視線と正四面体の交点が△OCAに含まれるか
t3 = ((k+m-sqrt(2.0/3.0)*s)/sqrt(2.0) + sqrt(3.0)*eye_pos_x)/(-sqrt(3.0)*(x_on_paper - eye_pos_x) + y_on_paper + m / sqrt(2.0));
x = ax * t3 + bx;
y = ay * t3 + by;
z = az * t3 + bz;
if( z < 0.0
|| -x/sqrt(3.0)+y > 0.0
|| x < 0.0
){
t3 = (m+k)/m;
}
// 対称物体上の点の位置を算出
float t = t1;
if( t > t2 ){
t = t2;
}
if( t > t3 ){
t = t3;
}
x = ax * t + bx;
y = ay * t + by;
z = az * t + bz;
PVector result = new PVector(x,y,z);
return result;
}