ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.16,17に掲載されている、カオスゲームと題された6つの図形を再現してみました。
Contents
カオスゲーム
今回作成したカオスゲームと題された6つの図形です。


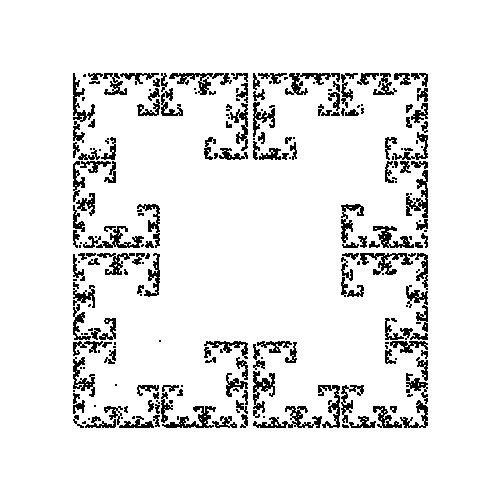

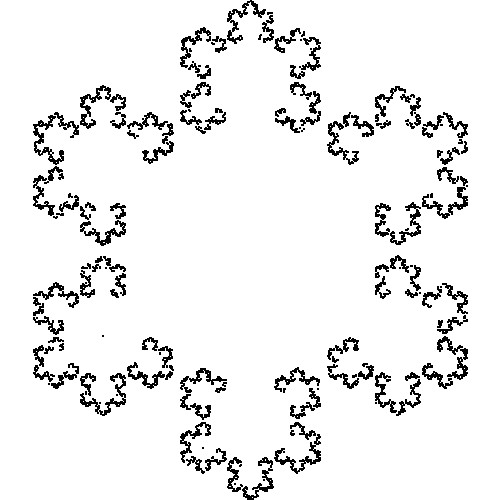

これらの図形はかなりシンプルなルールで描くことができます。以下で各図形の描き方とプロブラムコードを紹介します。
カオスゲーム(i)の描き方とプログラムコード
カオスゲーム(i)の描き方は以下の通りです。
STEP1:3つの頂点A,B,Cを正三角形の形に並べます。
STEP2:正三角形の内部の任意の点Pを1つ選びます。今回は正三角形の重心を選びました。
STEP3:3つの頂点A,B,Cからランダムに1つの頂点を選び、点Pから選ばれた頂点の方向でその長さの51%の位置に点Pを移動し、その位置に点をプロットします。
STEP4:あとは、STEP3を繰り返していくことでカオスゲーム(i)の図形を描くことができます。
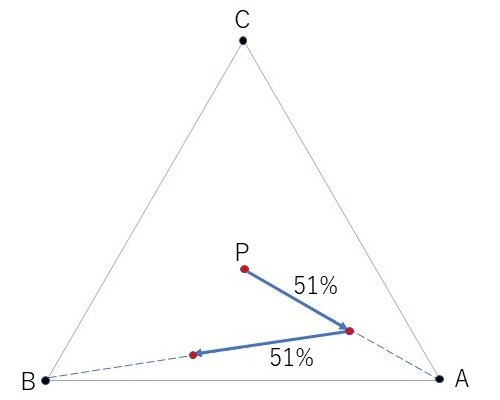
以下にプログラムコードを示します。今回は繰り返し回数を10000回としました。
float move_rate = 0.55; // 移動率
int step_num = 10000; // 繰り返し回数
void setup(){
size(500,500);
background(255,255,255);
translate(width/2.0, height/2.0);
// 正三角形の3点を取る
PVector[] flags = new PVector[3];
for(int i=0; i<3; i++){
flags[i] = PVector.fromAngle(radians(30+120*i)).mult(width/2.0);
}
PVector present_position = new PVector(0.0,0.0); // 移動先の位置
int i=0;
while(i<step_num){
present_position = present_position.copy().add(flags[int(random(3))].copy().sub(present_position.copy()).mult(move_rate));
rect(present_position.x,present_position.y, 1,1);
i++;
}
}カオスゲーム(ii)の描き方とプログラムコード
カオスゲーム(ii)の描き方は以下の通りです。
STEP1:4つの頂点A,B,C,Dを正方形の形に並べます。
STEP2:正方形の内部の任意の点Pを1つ選びます。今回は正方形の重心を選びました。
STEP3:4つの頂点A,B,C,Dからランダムに1つの頂点を選び、点Pから選ばれた頂点の方向でその長さの51%の位置に点Pを移動し、その位置に点をプロットします。
STEP4:4つの頂点A,B,C,Dからランダムに1つの頂点を選びます。このとき、前のSTEPで選ばれた頂点と異なる頂点が選ばれるようにします。点Pから選ばれた頂点の方向でその長さの51%の位置に点Pを移動し、その位置に点をプロットします。
STEP5:あとは、STEP4を繰り返していくことでカオスゲーム(ii)の図形を描くことができます。
以下にカオスゲーム(ii)のプログラムコードを示します。
float move_rate = 0.51; // 移動率
int step_num = 10000; // 繰り返し回数
void setup(){
size(500,500);
background(255,255,255);
translate(width/2.0, height/2.0);
// 正方形の頂点4点を取る
PVector[] flags = new PVector[4];
for(int i=0; i<4; i++){
flags[i] = PVector.fromAngle(radians(45+90*i)).mult(width/2.0);
}
PVector present_position = new PVector(0.0,0.0); // 移動先の位置
int i=0;
int number = 0; // 選択された頂点の番号
int previous_number = 0; // 前のSTEPで選択された頂点の番号
while(i<step_num){
number = int(random(4));
// 同じ頂点に向かって2回連続での移動禁止
if(number == previous_number){
continue;
}
present_position = present_position.copy().add(flags[number].copy().sub(present_position.copy()).mult(move_rate));
rect(present_position.x,present_position.y, 1,1);
previous_number = number;
i++;
}
}カオスゲーム(iii)の描き方とプログラムコード
カオスゲーム(iii)の描き方は以下の通りです。
STEP1:4つの頂点A,B,C,Dを正方形の形に並べます。
STEP2:正方形の内部の任意の点Pを1つ選びます。今回は正方形の重心を選びました。
STEP3:4つの頂点A,B,C,Dからランダムに1つの頂点を選び、点Pから選ばれた頂点の方向でその長さの51%の位置に点Pを移動し、その位置に点をプロットします。
STEP4:4つの頂点A,B,C,Dからランダムに1つの頂点を選びます。このとき、前のSTEPで選ばれた頂点に対して対角線上に位置する頂点が選ばれないようにします。点Pから選ばれた頂点の方向でその長さの51%の位置に点Pを移動し、その位置に点をプロットします。
STEP5:あとは、STEP4を繰り返していくことでカオスゲーム(iii)の図形を描くことができます。
以下にカオスゲーム(iii)のプログラムコードを示します。
float move_rate = 0.51; // 移動率
int step_num = 10000; // 繰り返し回数
void setup(){
size(500,500);
background(255,255,255);
translate(width/2.0, height/2.0);
// 正方形の頂点4点を取る
PVector[] flags = new PVector[4];
for(int i=0; i<4; i++){
flags[i] = PVector.fromAngle(radians(45+90*i)).mult(width/2.0);
}
PVector present_position = new PVector(0.0,0.0); // 移動先の位置
int i=0;
int number = 0; // 選択された頂点の番号
int previous_number = 0; // 前のSTEPで選択された頂点の番号
while(i<step_num){
number = int(random(4));
// 前の頂点の対角線上の頂点への移動禁止
if(number == (previous_number+2)%4){
continue;
}
present_position = present_position.copy().add(flags[number].copy().sub(present_position.copy()).mult(move_rate));
rect(present_position.x,present_position.y, 1,1);
previous_number = number;
i++;
}
}カオスゲーム(iv)の描き方とプログラムコード
カオスゲーム(iv)の描き方は以下の通りです。
STEP1:6つの頂点A,B,C,D,E,Fを正六角形の形に並べます。
STEP2:正六角形の内部の任意の点Pを1つ選びます。今回は正六角形の重心を選びました。
STEP3:6つの頂点A,B,C,D,E,Fからランダムに1つの頂点を選び、点Pから選ばれた頂点の方向でその長さの65%の位置に点Pを移動し、その位置に点をプロットします。
STEP4:6つの頂点A,B,C,D,E,Fからランダムに1つの頂点を選びます。このとき、前のSTEPで選ばれた頂点と異なる頂点が選ばれるようにします。点Pから選ばれた頂点の方向でその長さの65%の位置に点Pを移動し、その位置に点をプロットします。
STEP5:あとは、STEP4を繰り返していくことでカオスゲーム(iv)の図形を描くことができます。
以下にカオスゲーム(iv)のプログラムコードを示します。
float move_rate = 0.65; // 移動率
int step_num = 10000; // 繰り返し回数
void setup(){
size(500,500);
background(255,255,255);
translate(width/2.0, height/2.0);
// 正六角形の頂点6点を取る
PVector[] flags = new PVector[6];
for(int i=0; i<6; i++){
flags[i] = PVector.fromAngle(radians(30+60*i)).mult(width/2.0);
}
PVector present_position = new PVector(0.0,0.0); // 移動先の位置
int i=0;
int number = 0; // 選択された頂点の番号
int previous_number = 0; // 前のSTEPで選択された頂点の番号
while(i<step_num){
number = int(random(6));
// 同じ頂点に向かって2回連続での移動禁止
if(number == previous_number){
continue;
}
present_position = present_position.copy().add(flags[number].copy().sub(present_position.copy()).mult(move_rate));
rect(present_position.x,present_position.y, 1,1);
previous_number = number;
i++;
}
}カオスゲーム(v)の描き方とプログラムコード
カオスゲーム(v)の描き方は以下の通りです。
STEP1:6つの頂点A,B,C,D,E,Fを正六角形の形に並べます。
STEP2:正六角形の内部の任意の点Pを1つ選びます。今回は正六角形の重心を選びました。
STEP3:6つの頂点A,B,C,D,E,Fからランダムに1つの頂点を選び、点Pから選ばれた頂点の方向でその長さの68%の位置に点Pを移動し、その位置に点をプロットします。
STEP4:6つの頂点A,B,C,D,E,Fからランダムに1つの頂点を選びます。このとき、前のSTEPで選ばれた頂点に対して真向いにある頂点が選ばれないようにします。点Pから選ばれた頂点の方向でその長さの68%の位置に点Pを移動し、その位置に点をプロットします。
STEP5:あとは、STEP4を繰り返していくことでカオスゲーム(v)の図形を描くことができます。
以下にカオスゲーム(v)のプログラムコードを示します。
float move_rate = 0.68; // 移動率
int step_num = 10000; // 繰り返し回数
void setup(){
size(500,500);
background(255,255,255);
translate(width/2.0, height/2.0);
// 正六角形の頂点6点を取る
PVector[] flags = new PVector[6];
for(int i=0; i<6; i++){
flags[i] = PVector.fromAngle(radians(30+60*i)).mult(width/2.0);
}
PVector present_position = new PVector(0.0,0.0); // 移動先の位置
int i=0;
int number = 0; // 選択された頂点の番号
int previous_number = 0; // 前のSTEPで選択された頂点の番号
while(i<step_num){
number = int(random(6));
// 前の頂点の真向かいの頂点への移動禁止
if(number == (previous_number+3)%6){
continue;
}
present_position = present_position.copy().add(flags[number].copy().sub(present_position.copy()).mult(move_rate));
rect(present_position.x,present_position.y, 1,1);
previous_number = number;
i++;
}
}カオスゲーム(vi)の描き方とプログラムコード
カオスゲーム(vi)の描き方は以下の通りです。
STEP1:4つの頂点A,B,C,Dを正方形の形に並べます。
STEP2:正方形の内部の任意の点Pを1つ選びます。今回は正方形の重心を選びました。
STEP3:4つの頂点A,B,C,Dからランダムに1つの頂点を選び、点Pから選ばれた頂点の方向でその長さの51%の位置に点Pを移動し、その位置に点をプロットします。ただし、移動先の点Pが禁止領域(今回は重心を中心とし、直径が正方形の一辺の3分の1の大きさの円としています)に入る場合はプロットする前に点Pの位置を選び直します。
STEP4:あとは、STEP3を繰り返していくことでカオスゲーム(vi)の図形を描くことができます。
以下にカオスゲーム(vi)のプログラムコードを示します。
float move_rate = 0.51; // 移動率
int step_num = 10000; // 繰り返し回数
void setup(){
size(500,500);
background(255,255,255);
translate(width/2.0, height/2.0);
// 正方形の頂点4点を取る
PVector[] flags = new PVector[4];
for(int i=0; i<4; i++){
flags[i] = PVector.fromAngle(radians(45+90*i)).mult(width/2.0);
}
PVector present_position = new PVector(0.0,0.0); // 移動先の位置
PVector present_position_temp;
int i=0;
float forbidden_region_radius = width/2.0/3.0; // 禁止領域の半径
PVector center = new PVector(0.0,0.0);
while(i<step_num){
present_position_temp = present_position.copy().add(flags[int(random(4))].copy().sub(present_position.copy()).mult(move_rate));
// 中央の円内は入らない
if(present_position_temp.dist(center) < forbidden_region_radius){
continue;
}
present_position = present_position_temp.copy();
rect(present_position.x,present_position.y, 1,1);
i++;
}
// 禁止領域の灰色の円を描く
fill(230,230,230);
noStroke();
circle(0.0, 0.0, 2.0*forbidden_region_radius);
}