ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.12,13に掲載されている、シェルピンスキーのカーペット、ヴィチェクのカーペット、シェルピンスキーのギャスケット、シェルピンスキーのドイリーを作ってみました。
Contents
シェルピンスキーのカーペット
今回作成したシェルピンスキーのカーペットです。

シェルピンスキーのカーペットの作り方
シェルピンスキーのカーペットは以下の手順で作成できます。
- まず、中が詰まった正方形を描きます。
- その正方形を面積が等しい9個の正方形に分割します。
- 3×3に並んだ正方形の真ん中の1つを取り除きます。
- 2,3の手順を残った8個の正方形に対して実施します。
プログラムのポイント
作成手順は上記になりますが、実際にプログラムを書くときは「9個に分割して1個を取り除く」というより、「9個に分割して8個を描く」というやり方で行いました。
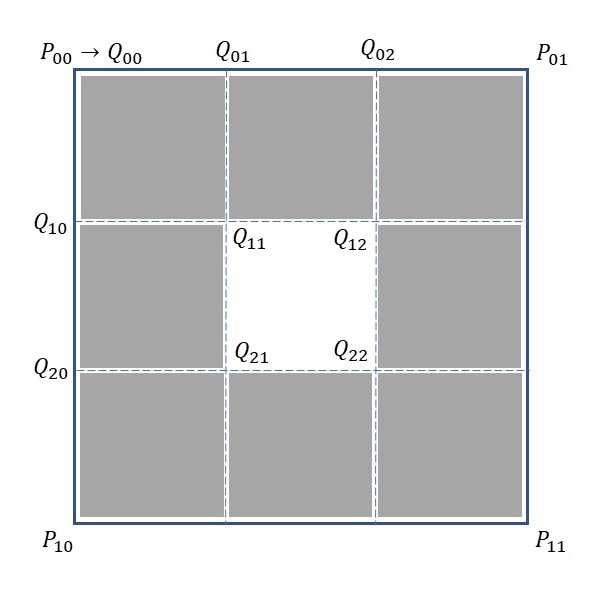
Processingで長方形を描くとき、rect関数を利用することができます。rect関数は長方形の左上の頂点と縦横の長さを指定することで長方形を描くことができます。つまり、以下の図のように左上の頂点を算出することで、分割した8個の正方形を描くことができます。
元の正方形の4つの頂点を\(P_{00},P_{01},P_{10},P_{11}\)で表すと、分割した9個の正方形の左上の頂点は\(Q_{00}\)~\(Q_{22}\) のような位置になります。分割した正方形の一辺の長さは元の正方形の一辺の長さの3分の1になるので、後はrect関数を用いて\(Q_{11}\)を左上の頂点とする正方形を除いた8個の正方形を描けばいいだけです。
プログラムコード
シェルピンスキーのカーペットを描くプログラムコードを載せておきます。
float h_min = 10.0; // 正方形一辺の長さの最小値
void setup(){
size(500,500);
background(255,255,255);
// シェルピンスキーのカーペットを描く
stroke(100,100,100);
fill(100,100,100);
PVector start = new PVector(0.0,0.0);
drawSierpinskiCarpet(start, width);
}
// シェルピンスキーカーペットを作る関数
void drawSierpinskiCarpet(PVector start, float side_length){
// 正方形を同じ面積の正方形9個に分けるための頂点
PVector[][] vertices = new PVector[3][3];
for(int i=0; i<3; i++){
for(int j=0; j<3; j++){
vertices[i][j] = new PVector(i * side_length / 3.0, j * side_length / 3.0);
vertices[i][j].add(start.copy());
}
}
// 正方形を再帰的に描画する
if(side_length > h_min){
for(int i=0; i<3; i++){
for(int j=0; j<3; j++){
if(i != 1 || j != 1){
drawSierpinskiCarpet(vertices[i][j], side_length/3.0);
}
}
}
} else {
for(int i=0; i<3; i++){
for(int j=0; j<3; j++){
if(i != 1 || j != 1){
rect(vertices[i][j].x, vertices[i][j].y, side_length/3.0, side_length/3.0);
}
}
}
}
}ヴィチェクのカーペット
次に、ヴィチェクのカーペットを作成しました。

ヴィチェクのカーペットの作り方
ヴィチェクのカーペットは以下の手順で作成できます。
- まず、中が詰まった正方形を描きます。
- その正方形を面積が等しい9個の正方形に分割します。
- 3×3に並んだ正方形の四隅4つを取り除きます。
- 2,3の手順を残った5個の正方形に対して実施します。
シェルピンスキーのカーペットと似ています。
プログラムのポイント
シェルピンスキーのカーペットと同様に、実際にプログラムを書くときは「9個に分割して4個を取り除く」というより、「9個に分割して5個を描く」というやり方で行いました。
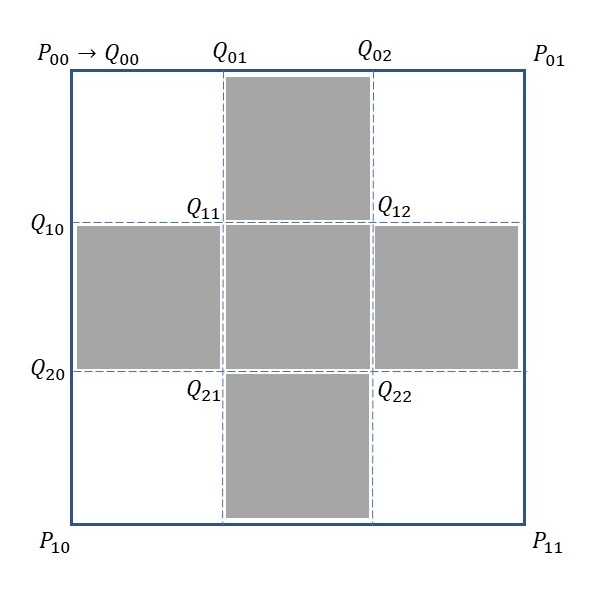
元の正方形の4つの頂点を\(P_{00},P_{01},P_{10},P_{11}\)で表すと、分割した9個の正方形の左上の頂点は\(Q_{00}\)~\(Q_{22}\) のような位置になります。分割した正方形の一辺の長さは元の正方形の一辺の長さの3分の1になるので、後はrect関数を用いて\(Q_{00},Q_{02},Q_{20},Q_{22}\)を左上の頂点とする正方形4個を除いた5個の正方形を描けばいいだけです。
プログラムコード
ヴィチェクのカーペットを描くプログラムコードを載せておきます。
float h_min = 10.0; // 正方形一辺の長さの最小値
void setup(){
size(500,500);
background(255,255,255);
// ヴィチェックのカーペットを描く
stroke(100,100,100);
fill(100,100,100);
PVector start = new PVector(0.0,0.0);
drawWiteczekCarpet(start, width);
}
// ヴィチェックのカーペットを作る関数
void drawWiteczekCarpet(PVector start, float side_length){
// 正方形を同じ面積の正方形9個に分けるための頂点
PVector[][] vertices = new PVector[3][3];
for(int i=0; i<3; i++){
for(int j=0; j<3; j++){
vertices[i][j] = new PVector(i * side_length / 3.0, j * side_length / 3.0);
vertices[i][j].add(start.copy());
}
}
// 正方形を再帰的に描画する
if(side_length > h_min){
drawWiteczekCarpet(vertices[0][1], side_length/3.0);
for(int j=0; j<3; j++){
drawWiteczekCarpet(vertices[1][j], side_length/3.0);
}
drawWiteczekCarpet(vertices[2][1], side_length/3.0);
} else {
rect(vertices[0][1].x, vertices[0][1].y, side_length/3.0, side_length/3.0);
for(int j=0; j<3; j++){
rect(vertices[1][j].x, vertices[1][j].y, side_length/3.0, side_length/3.0);
}
rect(vertices[2][1].x, vertices[2][1].y, side_length/3.0, side_length/3.0);
}
}シェルピンスキーのギャスケット
シェルピンスキーのギャスケットは以下のような図形です。

シェルピンスキーのギャスケットの作り方
シェルピンスキーのギャスケットは以下の手順で作成できます。
- まず、中が詰まった正三角形を描きます。
- その正三角形を面積が等しい4個の正三角形に分割します。
- 4つの正三角形のうち、真ん中の1つを取り除きます。
- 2,3の手順を残った3個の正三角形に対して実施します。
プログラムのポイント
シェルピンスキーのギャスケットも、実際にプログラムを書くときは「4個に分割して1個を取り除く」というより、「4個に分割して3個を描く」というやり方で行いました。
Processingで三角形を描くとき、triangle関数を利用することができます。triangle関数は三角形の3つの頂点の位置を指定することで三角形を描くことができます。今回描く正三角形では、その重心位置と重心から正三角形の3つの頂点までの距離を与えることで3つの頂点の位置を算出するようにしています。これは正三角形を分割して描く際に重心位置を基準にして考えた方が描きやすいと思ったからです。
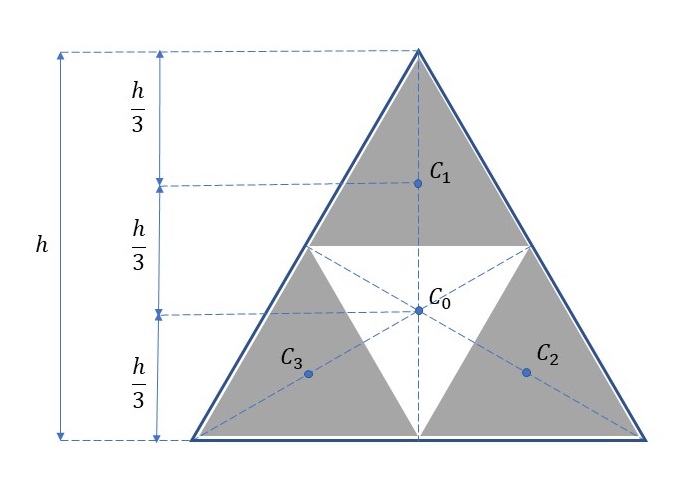
元の正三角形の重心を\(C_0\)、高さを\(h\)で表すと、分割した4個の正三角形の重心は下図の\(C_0\)~\(C_3\)のような位置に現れます。\(C_1,C_2,C_3\)の位置は元の正三角形の重心位置から\(h\)の3分の1の距離に位置します。また、分割した正三角形の重心から各頂点までの距離は\(h/3\)となるので、3つの頂点の位置を算出することができます。後はtriangle関数を用いて\(C_0\)を重心とする正三角形を除いた残り3つの正三角形を描けばいいだけです。
プログラムコード
シェルピンスキーのギャスケットを描くプログラムコードを載せておきます。
float h_min = 10.0; // // 正三角形の一辺の長さの最小値
void setup(){
size(500,500);
background(255,255,255);
// シェルピンスキーのギャスケットを描く
stroke(100,100,100);
fill(100,100,100);
PVector center_of_gravity = new PVector(width/2.0,height * 2.0/3.0);
drawSierpinskiGasket(center_of_gravity, width);
}
// シェルピンスキーのギャスケットを作る関数
void drawSierpinskiGasket(PVector center_of_gravity, float side_length){
// 分割した正三角形3つの重心
PVector[] cogs = new PVector[3];
for(int i=0; i<3; i++){
cogs[i] = PVector.fromAngle(radians(-90+120.0*i)).mult(side_length/sqrt(3.0)/2.0).add(center_of_gravity.copy());
}
// 正三角形を再帰的に描画する
if(side_length > h_min){
for(int i=0; i<3; i++){
drawSierpinskiGasket(cogs[i], side_length/2.0);
}
} else {
for(int i=0; i<3; i++){
drawEquilateralTriangle(cogs[i], side_length/2.0);
}
}
}
// 正三角形を描く関数
void drawEquilateralTriangle(PVector center_of_gravity, float side_length){
// 正三角形の頂点
PVector[] vertices = new PVector[3];
for(int i=0; i<3; i++){
vertices[i] = PVector.fromAngle(radians(-90+120.0*i)).mult(side_length/sqrt(3.0)).add(center_of_gravity.copy());
}
// 正三角形を描く
triangle(vertices[0].x, vertices[0].y, vertices[1].x, vertices[1].y, vertices[2].x, vertices[2].y);
}シェルピンスキーのドイリー
シェルピンスキーのドイリーは以下のような図形です。

シェルピンスキーのドイリーの作り方
シェルピンスキーのドイリーは以下の手順で作成できます。
- まず、中が詰まった正六角形を描きます。
- その正六角形を以下の図のように面積が等しい7個の正六角形と面積が等しい12個の正三角形に分割します。
- 7つの正六角形のうち真ん中の1つ、および12個の正三角形をすべて取り除きます。
- 2,3の手順を残った6個の正六角形に対して実施します。

プログラムのポイント
シェルピンスキーのドイリーも、実際にプログラムを書くときは「正六角形7個と正三角形12個に分割して正六角形1個と正三角形全てを取り除く」というより、「正六角形6個を描く」というやり方で行いました。
Processingで正六角形を描くときは、beginShape関数とendShape関数を利用することができます(詳細は別記事「任意の図形を描く」をみてください)。これらの関数の間に図形の頂点を順に示していくことで任意の図形を描くことができます。今回描く正六角形では、その重心位置と重心から正六角形の6つの頂点までの距離を与えることで6つの頂点の位置を算出するようにしています。これは正六角形を分割して描く際に重心位置を基準にして考えた方が描きやすいと思ったからです。
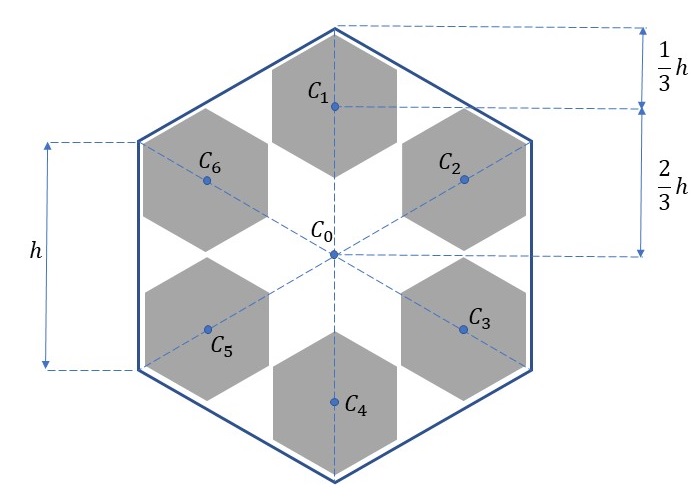
元の正六角形の重心を\(C_0\)、一辺の長さを\(h\)で表すと、分割した7個の正六角形の重心は下図の\(C_0\)~\(C_6\)のような位置に現れます。\(C_1\)~\(C_6\)の位置は元の正六角形の重心位置から\(h\)の3分の2の距離に位置します。また、分割した正六角形は、その重心から各頂点までの距離が\(h/3\)となるので、6つの頂点の位置を算出することができます。後はbeginShape関数とendShape関数を用いて\(C_0\)を重心とする正六角形を除いた残り6つの正六角形を描けばいいだけです。
プログラムコード
シェルピンスキーのドイリーを描くプログラムコードを載せておきます。
float h_min = 5.0; // 一辺の長さの最小値
void setup(){
size(500,500);
background(255,255,255);
// シェルピンスキーのドイリーを描く
stroke(100,100,100);
fill(100,100,100);
PVector center_of_gravity = new PVector(width/2.0,height/2.0);
drawSierpinskiDoily(center_of_gravity, width/2.0);
}
// シェルピンスキーのドイリーを作る関数
void drawSierpinskiDoily(PVector center_of_gravity, float side_length){
// 分割した正六角形6つの重心
PVector[] cogs = new PVector[6];
for(int i=0; i<6; i++){
cogs[i] = PVector.fromAngle(radians(-90+60.0*i)).mult(side_length * 2.0/3.0).add(center_of_gravity.copy());
}
// 正六角形を再帰的に描画する
if(side_length > h_min){
for(int i=0; i<6; i++){
drawSierpinskiDoily(cogs[i], side_length/3.0);
}
} else {
for(int i=0; i<6; i++){
drawHexagon(cogs[i], side_length/3.0);
}
}
}
// 正六角形を描く関数
void drawHexagon(PVector center_of_gravity, float side_length){
// 正六角形の頂点
PVector[] vertices = new PVector[6];
for(int i=0; i<6; i++){
vertices[i] = PVector.fromAngle(radians(-90+60.0*i)).mult(side_length).add(center_of_gravity.copy());
}
// 正六角形を描く
beginShape();
for(int i=0; i<6; i++){
vertex(vertices[i].x,vertices[i].y);
}
endShape(CLOSE);
}