ここでは、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.4,5に掲載されていたコッホ曲線やコッホ雪片について、自分でも作ってみました。
コッホ曲線
まず、コッホ雪片を作るための基礎となる、コッホ曲線について解説します。
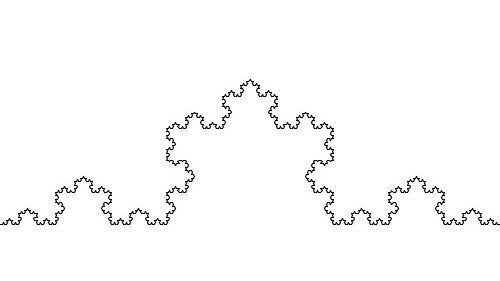
コッホ曲線の描き方
このコッホ曲線の描き方を説明します。なお、書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.4にある解説そのままです。
- 1本の線分を引く。
- 次に真ん中の3分の1を正三角形から底辺を除いた”テント”にして、長さの等しい4本の線分にする。
- 同じ操作を4本の線分すべてで再度行う。
これを繰り返すことでコッホ曲線を描くことができます。
プログラムコード
コッホ曲線を描くためのプログラムコードを載せておきます。上記の解説では「線分を引いて、真ん中の3分の1を削除してテントに置き換える」となっていますが、実際のプログラムで「一度描いて、一部削除」は余計な処理になりますので、今回のプログラムでは「再帰的な呼び出し処理の最後にコッホ曲線を描く」ようにしています。
float h_min = 10.0; // 枝の長さの最小値
void setup(){
size(500,500);
background(255,255,255);
// コッホ曲線
PVector start = new PVector(0.0, height*2.0/3.0);
PVector end = new PVector(width, height*2.0/3.0);
drawKoch(start, end);
}
// コッホ曲線を描くための関数
void drawKoch(PVector start, PVector end){
// startとendで結ばれる線分を3分割する点
PVector sub_vec = end.copy().sub(start.copy());
PVector sep_point1 = PVector.add(start.copy(), sub_vec.copy().mult(1.0/3.0));
PVector sep_point2 = PVector.add(start.copy(), sub_vec.copy().mult(2.0/3.0));
PVector koch_point = PVector.add(sep_point1.copy(), sub_vec.copy().mult(1.0/3.0).rotate(radians(-60)));
// コッホ曲線を再帰的に描画する
if(sub_vec.mag() > h_min){
drawKoch(start, sep_point1);
drawKoch(sep_point1, koch_point);
drawKoch(koch_point, sep_point2);
drawKoch(sep_point2, end);
} else {
line(start.x, start.y, sep_point1.x, sep_point1.y);
line(sep_point1.x, sep_point1.y, koch_point.x, koch_point.y);
line(koch_point.x, koch_point.y, sep_point2.x, sep_point2.y);
line(sep_point2.x, sep_point2.y, end.x, end.y);
}
} コッホ雪片
コッホ雪片は正三角形を描き、3辺それぞれをコッホ曲線で置き換えることで描くことができます。

プログラムコード
コッホ雪片を描くためのプログラムコードを載せておきます。コッホ曲線ではline関数を用いて描きましたが、コッホ雪片では図形の塗りつぶしのことも考えて、テントの部分をtriangle関数を用いて描いています。
float h_min = 10.0; // 枝の長さの最小値
void setup(){
size(500,500);
background(255,255,255);
translate(width/2, height/2);
rotate(radians(30));
// コッホ雪片を描く
stroke(100,100,100);
fill(100,100,100);
drawSnowFlake(width/3.0);
}
// コッホ雪片を作る関数
void drawSnowFlake(float radius){
// 最初の段階の三角形の頂点
PVector[] vertices = new PVector[3];
vertices[0] = PVector.fromAngle(radians(-90)).mult(radius);
vertices[1] = PVector.fromAngle(radians(30)).mult(radius);
vertices[2] = PVector.fromAngle(radians(150)).mult(radius);
triangle(
vertices[0].x, vertices[0].y,
vertices[1].x, vertices[1].y,
vertices[2].x, vertices[2].y
);
drawKoch(vertices[0], vertices[1]);
drawKoch(vertices[1], vertices[2]);
drawKoch(vertices[2], vertices[0]);
}
// コッホ雪片を作るためのコッホ曲線
void drawKoch(PVector start, PVector end){
// startとendで結ばれる線分を3分割する点
PVector sub_vec = end.copy().sub(start.copy());
PVector sep_point1 = PVector.add(start.copy(), sub_vec.copy().mult(1.0/3.0));
PVector sep_point2 = PVector.add(start.copy(), sub_vec.copy().mult(2.0/3.0));
PVector koch_point = PVector.add(sep_point1.copy(), sub_vec.copy().mult(1.0/3.0).rotate(radians(-60)));
// sep_point1とsep_point2, koch_pointを頂点とする三角形を描く
triangle(
sep_point1.x, sep_point1.y,
koch_point.x, koch_point.y,
sep_point2.x, sep_point2.y
);
// コッホ曲線を再帰的に描画する
if(sub_vec.mag() > h_min){
drawKoch(start, sep_point1);
drawKoch(sep_point1, koch_point);
drawKoch(koch_point, sep_point2);
drawKoch(sep_point2, end);
}
}
コッホ雪片を用いた図形
書籍「フラクタル: 混沌と秩序のあいだに生まれる美しい図形 アルケミスト双書」のp.5にある、コッホ雪片を用いた図形を再現してみました。



コッホ雪片を用いた図形