この記事では書籍「世界一美しい錯視アート」に掲載されている「不可能図形的蛇の回転2」という作品をProcessingを使って再現してみます。
不可能図形的蛇の回転2
今回作成した錯視アート「不可能図形的蛇の回転2」です。

書籍では「内側のリングは時計回りに、外側のリングは反時計回りに回転して見える。」と解説されています。じっと見ていると、そのように見えてくるので不思議です。
描き方のポイント
爪型図形の描き方
この作品の1番のポイントは円環上に並んだ、爪型図形の描き方だと思います。ここでは、爪型図形をどのように描いていったかを解説していきます。そのために以下の図のようにパラメータを設定します。
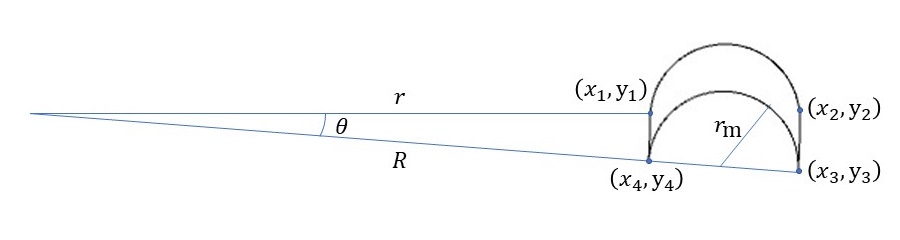
円環の外側の円の半径を\(R\)、内側の円の半径を\(r\)とします。このとき、爪型を表す半円の半径は\[ r_{\mathrm{m}} = \frac{R+r}{2} \]となります。また爪型の幅を角度\(\theta\)で表します。このとき、図の各座標はそれぞれ
\[ x_1 = r, \ \ y_1=0, \ \ x_2=R, \ \ y_2=0, \ \ x_3=R \cos \theta, \ \ y_3=R \sin \theta, \ \ x_4= r \cos \theta, \ \ y_4=r \sin \theta \]
となります。ここまで準備ができたら、以下の手順で爪型の図形を描くことができます。
- 点\((x_1,y_1)\)から点\((x_2,y_2)\)までを結ぶ、半径\(r_{\mathrm{m}}\)の半円を描きます。
- 点\((x_2,y_2)\)から点\((x_3,y_3)\)までを結ぶ、半径\(R\)の円弧を描きます。
- 点\((x_3,y_3)\)から点\((x_4,y_4)\)までを結ぶ、半径\(r_{\mathrm{m}}\)の半円を描きます。
- 点\((x_4,y_4)\)から点\((x_1,y_1)\)までを結ぶ、半径\(r\)の円弧を描きます。
これで爪型図形は完成するので、あとは大きさを調整し、色を白色や黒色にしたり黄色や青色でグラデーションさせたりしたものを円環状に並べていくことでこの作品を作ることができます。
プログラムコード
今回作成した錯視アート「不可能図形的蛇の回転2」のプログラムコードを載せておきます。
void setup() {
size(1000, 1000);
background(255,255,255);
noStroke();
translate(width/2, height/2);
float annulus_R = width/2.0; // 円環の大半径
float ratio = 0.8; // 円環の大半径と小半径の比
int parts_num = 36; // パーツの個数
float theta = radians(360)/parts_num;
// 大きい(外側の)円環を描画
for(int i=0; i<parts_num; i++){
drawNail_grad(annulus_R, ratio, theta * 0.4, color(255,255,0), color(200,200,0));
rotate(theta * 0.4);
drawNail(annulus_R, ratio, theta * 0.1, color(255,255,255));
rotate(theta * 0.1);
drawNail_grad(annulus_R, ratio, theta * 0.4, color(0,0,255), color(0,0,200));
rotate(theta * 0.4);
drawNail(annulus_R, ratio, theta * 0.1, color(0,0,0));
rotate(theta * 0.1);
}
// 小さい(内側の)円環を描画
scale(-1,1);
annulus_R = 0.75 * annulus_R; // 円環の大半径の大きさを更新
for(int i=0; i<parts_num; i++){
drawNail_grad(annulus_R, ratio, theta * 0.4, color(255,255,0), color(200,200,0));
rotate(theta * 0.4);
drawNail(annulus_R, ratio, theta * 0.1, color(255,255,255));
rotate(theta * 0.1);
drawNail_grad(annulus_R, ratio, theta * 0.4, color(0,0,255), color(0,0,200));
rotate(theta * 0.4);
drawNail(annulus_R, ratio, theta * 0.1, color(0,0,0));
rotate(theta * 0.1);
}
}
// 爪の形状を描く関数
void drawNail(
float annulus_R, // 円環の大半径
float ratio, // 円環の大半径と小半径の比
float theta, // 爪の幅に対応する角度
color fill_color // 爪の色
){
float annulus_r = annulus_R * ratio; // 円環の小半径
float semicircle_radius = (annulus_R - annulus_r)/2.0; // 円環上に並ぶ半円の半径
float mid_radius = annulus_r + semicircle_radius; // 円環の真ん中の半径
fill(fill_color);
float center_x = mid_radius;
float center_y = 0.0;
float x, y;
beginShape();
for(int j=0; j<=100; j++){
x = center_x + semicircle_radius * cos(radians(180)+j*radians(180)/100.0);
y = center_y + semicircle_radius * sin(radians(180)+j*radians(180)/100.0);
vertex(x, y);
}
for(int j=1; j<10; j++){
x = annulus_R * cos(j * theta / 10.0);
y = annulus_R * sin(j * theta / 10.0);
vertex(x, y);
}
center_x = mid_radius * cos(theta);
center_y = mid_radius * sin(theta);
for(int j=0; j<=100; j++){
x = center_x + semicircle_radius * cos(theta-j*radians(180)/100.0);
y = center_y + semicircle_radius * sin(theta-j*radians(180)/100.0);
vertex(x, y);
}
for(int j=1; j<10; j++){
x = annulus_r * cos(theta - j * theta / 10.0);
y = annulus_r * sin(theta - j * theta / 10.0);
vertex(x, y);
}
endShape(CLOSE);
}
// 爪の形状を描く関数(グラデーションあり)
void drawNail_grad(
float annulus_R, // 円環の大半径
float ratio, // 円環の大半径と小半径の比
float theta, // 爪の幅に対応する角度
color color_out, // 爪の外側の色
color color_in // 爪の内側の色
){
float annulus_r = annulus_R * ratio; // 円環の小半径
float semicircle_radius = (annulus_R - annulus_r)/2.0; // 円環上に並ぶ半円の半径
float mid_radius = annulus_r + semicircle_radius; // 円環の真ん中の半径
float center_x, center_y;
float x, y, r, r_theta;
for(int i=0; i<=50; i++){
color col = lerpColor(color_out, color_in, i/50.0); // 色
fill(col);
beginShape();
center_x = mid_radius;
center_y = 0.0;
for(int j=-(50-i); j<=(50-i); j++){
x = center_x + semicircle_radius * cos(radians(270)+j*radians(180)/100.0);
y = center_y + semicircle_radius * sin(radians(270)+j*radians(180)/100.0);
vertex(x, y);
}
x = center_x + semicircle_radius * cos(radians(270)+(50-i)*radians(180)/100.0);
y = center_y + semicircle_radius * sin(radians(270)+(50-i)*radians(180)/100.0);
r = sqrt(x*x + y*y);
r_theta = atan2(y,x);
for(int j=1; j<10; j++){
x = r * cos(r_theta + j * theta / 10.0);
y = r * sin(r_theta + j * theta / 10.0);
vertex(x, y);
}
center_x = mid_radius * cos(theta);
center_y = mid_radius * sin(theta);
for(int j=-(50-i); j<=(50-i); j++){
x = center_x + semicircle_radius * cos(theta - radians(90) - j*radians(180)/100.0);
y = center_y + semicircle_radius * sin(theta - radians(90) - j*radians(180)/100.0);
vertex(x, y);
}
x = center_x + semicircle_radius * cos(theta - radians(90) - (50-i)*radians(180)/100.0);
y = center_y + semicircle_radius * sin(theta - radians(90) - (50-i)*radians(180)/100.0);
r = sqrt(x*x + y*y);
r_theta = atan2(y,x);
for(int j=1; j<10; j++){
x = r * cos(r_theta - j * theta / 10.0);
y = r * sin(r_theta - j * theta / 10.0);
vertex(x, y);
}
endShape(CLOSE);
}
}