最近、書籍「アートで魅せる数学の世界」のp.94に掲載されている「2種類以上の正多角形によるタイリング」を再現しようと今準備を進めているのですが、その過程でふと気づいたことがあります。それは、93種類のアイソヘドラルタイリングの中に、記事「基本図形の形を考える」で紹介したP4G群の基本図形に対応するものがないことです。
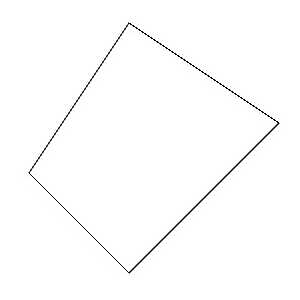
93種類のアイソヘドラルタイリングのうちP4G群の対称性をもつもので、上記の四角形が正方形となる場合に限定したものがIH56(P4G)となっていて、また、上記の四角形の一辺を縮めて直角二等辺三角形したものがIH81(P4G)となっていますが、上記の四角形をもつP4G群のアイソヘドラルタイリングはありませんでした。
個人的にはIH56(P4G)が正方形に限定されるものではなく、本来上記のような四角形を対象とするものなのではないかと考えていますが、今のところ正確なことはわかりません。
そこで、今回はIH56(P4G)の基本図形を正方形からもう少し形を変えた四角形を持つものと考え、記事「IH56(P4G)の拡張」として紹介しました。

記事「IH56(P4G)の拡張」で紹介したものが94番目のアイソヘドラルタイリングになるのか、そもそもIH56(P4G)の正規版になるのかはわかりません。ただ、すくなくとも、記事「IH56(P4G)の拡張」で紹介したものがないと、アイソヘドラルタイリングを網羅できないことは確かです。