今日は、書籍「アートで魅せる数学の世界」のp.30-31で紹介されているフィボナッチ長方形に合わせて疑似的な螺旋を描いた記事「フィボナッチ数列による螺旋」を公開しました。
今回描いたのは以下のような疑似的な螺旋です。
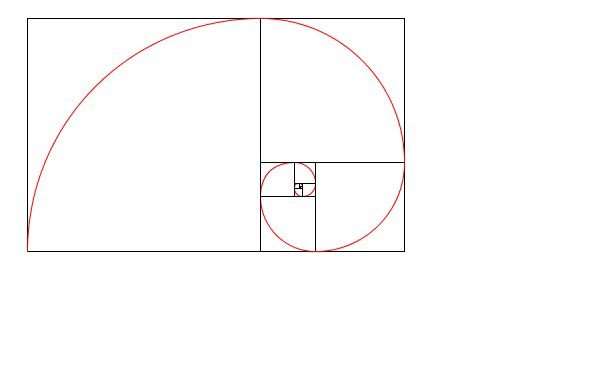
フィボナッチ数列による螺旋は、円弧をつないだ疑似的な螺旋です。その円弧を描く際に利用するarc関数について、1点注意が必要であることが分かりました。角度\(\theta_1\)から角度\(\theta_2\)までの円弧を描きたいときには、arc関数の5番目と6番目の引数にそれぞれ\(\theta_1\)と\(\theta_2\)を与えればいいわけですが、\(\theta_1 < \theta_2 \)となるように値を与えないと描けないようです。特にこだわりがなければ、\(\theta_1\)と\(\theta_2\)の順番を入れ替えればいいわけですが、一応知っておいても損はないと思います。