書籍「M.C.エッシャーと楽しむ算数・数学パズル」の「オシドリの模様その2」(p.48-53)を読んでいて、ふと自分の間違いに気づいてしまいました。
記事「基本図形を変形する」の「変形する際のルール」のところで、
『(4)両側のラベルが異なり、向きは同じとき、この辺は垂直二等分線に関して線対称な変形が可能です。』
ということを記載していました。
「オシドリの模様その2」はPGG群の対称性を持つので、基本図形(書籍「M.C.エッシャーと楽しむ算数・数学パズル」ではタイル)の辺はこの(4)のルールに従うはず。
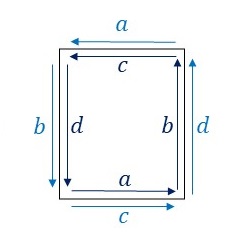
でも、「オシドリの模様その2」は明らかにそのルールに従っていない。にもかかわらず、PGG群の対称性はしっかりと満たしている。
というわけで、このルールが載っていた書籍「エッシャー・マジック―だまし絵の世界を数理で読み解く」の3.1節(p.40~p.44)を再度見直してみました。その結果、
私が完全に読み違えていました。
書籍「エッシャー・マジック―だまし絵の世界を数理で読み解く」のp.44から引用すると、
『(3) 両側のラベルが異なり、それぞれ一方向の向きをもつとき(図3.4(c))、このタイリング辺は自由に変形できます。このことは、向きが同じであっても、逆であってもなりたちます。
(4)両側のラベルが異なり、少なくとも一方の辺が両方向の向きをもつとき(このときはもう一方の辺も両方向の向きをもちます;図3.4(d))、このタイリング辺は垂直二等分線に関して線対称でなければなりません。』
と記載されていました。明らかに、
『(4)両側のラベルが異なり、向きは同じとき、この辺は垂直二等分線に関して線対称な変形が可能です。』
などとは記載されていません。
今後、記事「基本図形を変形する」の「変形する際のルール」を修正するとともに、それに関連した変形の例も修正していきたいと思います。
ただ、一点だけ疑問が。
『両方向の向きをもつ』という状態はどんなとき出てくるんだろうか?
これまでの例では一度も出てきたことがないんですが・・・。
数学アートを描き続ければ、いずれ出会うことができるかな。