出会ってしまった、数学アートの世界。世の中には美しい数学が多数あります。このサイトではそのような美しい数学を使って描ける美しいアートをその描き方とともに紹介していきたいと思います。

当サイトで紹介している各種数学アートに対する質問やコメントのある方は「お問い合わせ」からお願いします。

壁紙アート

壁紙とは位置を全体的にずらしたり、回転させたりしても模様が全く変わらないような図形のことを指します。ここではそのような性質を持った図形を数学的に分類して、それぞれの図形の描くための方法やそのプログラム（Processing）について紹介します。

エッシャーに挑戦！

ここでは、上記「壁紙アート」で解説してきたことを応用して、エッシャー風の絵を描いていきます。

錯視アート

書籍「世界一美しい錯視アート」で紹介されている作品を見て、自分でも作ってみたいと思いました。一つ一つの作品についてその再現方法やそのプログラム（Processing）について紹介していきます。

黄金比

ここでは、黄金比にまつわるいろいろな美しい図形を紹介しています。

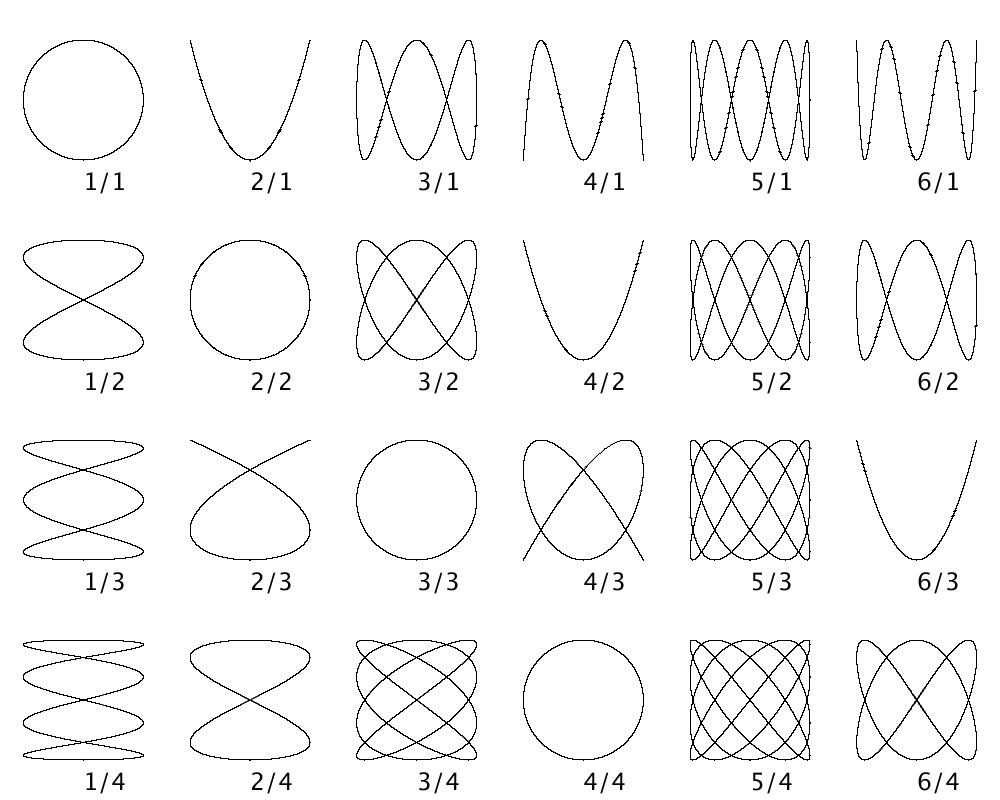
リサージュ図形

リサージュ図形とは、平面座標上の点\((x,y)\)の\(x\)と\(y\)それぞれに三角関数（\(\sin\)カーブや\(\cos\)カーブ）のような周期関数を印加して得られるベクトルの軌跡が描く図形のことです。周期関数を組み合わせることでさまざまな美しい図形を描くことができます。

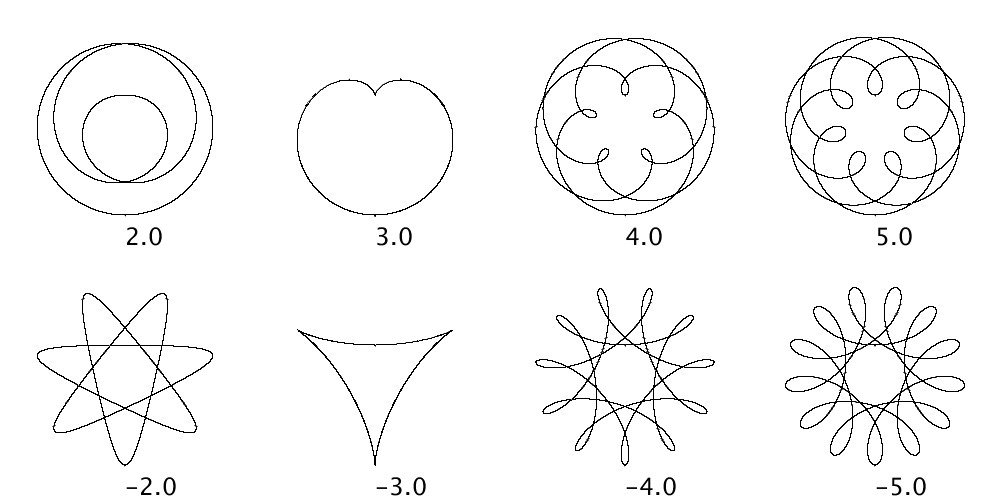
ストリング・アート

糸掛けという技術を応用したストリング・アート。工夫次第で様々な美しい図形を描くことができます。

フラクタル

マンデルブロー集合やジュリア集合などなど。フラクタルによる図形はすごく美しい図形です。でも、見ているだけでは物足りない。やっぱり自分でも描いてみたいと思いました。

TSPアート

書籍「マス・アート～真理、美、そして方程式～」で紹介されていたTSPアート。TSPとは「巡回セールスマン問題（traveling salesman problem）」のことです。このTSPを用いたアートに魅力を感じました。ただ、このTSPアート、自分でやってみるとすごく奥が深い。少しずつですが、いろいろ試行錯誤していった過程を残していきたいと思います。

立体視（ステレオグラム）

平面に描かれた図形をじっと見つめていると、平面なのに立体的な絵が浮かび上がってくる、とても不思議なアート。ここではそんな立体視（ステレオグラム）の描き方を紹介します。

計算手法でアート

世の中にはいろいろと便利な計算手法があります。そのような計算手法を用いてアートに挑戦しています。

Processingの使い方

このサイトで紹介している数学アートのほとんどはプログラミング言語「Processing」で描いています。ここではそのProcessingの使い方を紹介していきたいと思います。